К сожалению, на плоскости параметризуются многие, но далеко не все поверхности. Даже поверхности, параметризуемые на сфере, требуют совершенно иного подхода (если мы захотим смоделировать не участок земной поверхности, а земной шар целиком, то будем иметь дело как раз с такой поверхностью), а ведь даже ими не исчерпываются все виды поверхностей, с которыми приходится встречаться в приложениях.

В дальнейшем мы будем обсуждать только “общий” случай, когда параметризация на плоскости невозможна.

Если кривые задаются набором опорных точек, образующим опорный многоугольник, то поверхности задаются опорной сеткой (control mesh). По полной аналогии с кривыми поверхность может интерполировать опорную сетку (проходить через все ее узлы), аппроксимировать ее (не касаться узлов); возможны смешанные варианты. Наиболее простой способ представления поверхности (и, тем не менее, достаточно часто использующийся) — кусочно-билинейная интерполяция треугольной сетки.

Очевидно, что далеко не каждая сетка допускает многомасштабный анализ. Такой особенностью обладают только сетки, полученные с помощью некоторой схемы подразбиения (subdivision scheme).

Рассмотрим пример простой треугольной сетки  например, тетраэдра (Рис. 6). Разбиение осуществляется в два этапа. Сначала в середину каждого узла добавляется новый узел, новые узлы соединяются ребрами так, чтобы снова получилась треугольная сетка . Простейшая схема подразбиения — полиэдральная (polyhedral subdivision) — этим этапом и заканчивается. Понятно, что в пределе полиэдральное подразбиение дает ту же поверхность, что задавалась исходной сеткой. Второй этап не меняет структуру сетки, зато меняет пространственное расположение ее узлов по некоторому правилу. В случае интерполирующей схемы однажды зафиксированные узлы перемещать нельзя, поэтому “двигать” можно только вновь добавленные узлы (сетка ). В случае аппроксимирующей схемы меняется расположение “старых” узлов (сетка ). (Подробно о схемах подразбиения см. [1]).

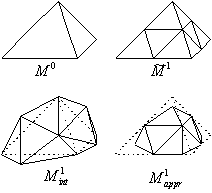
Если некоторая поверхность задается опорной сеткой , которую можно представить как результат применения некоторой схемы подразбиения, то очевидно, многомасштабным анализом такой сетки станет последовательность сеток . Каждая сетка  может быть разделена на низкочастотную составляющую  и детализирующую составляющую . Воспользуемся имеющимися обозначениями для операторов анализа () и синтеза () для записи соответствующих операций:

и .

К сожалению, обсуждение построения конкретных вейвлет-базисов выходит за рамки данного курса, заинтересовавшимся рекомендуем обратиться к [1, 4].

Сразу обратим внимание на следующую проблему: далеко не всегда поверхность задана сеткой, допускающей многомасштабный анализ. Например, при сканировании реальных трехмерных объектов, информация заносится в ЭВМ обычно в виде очень частых сеток, имеющих десятки тысяч треугольников. Переход от такой “произвольной” сетки, к представлению, допускающему многомасштабный анализ является непростой и трудоемкой задачей. Подробно эта проблема рассматривается в [3].

Автоматическое управление уровнем детализации. Часто оказывается неэффективной визуализация сложных трехмерных объектов с полным восстановлением всех деталей. Вот хотя бы некоторые подобные ситуации:

• разрешающая способность видеоустройства ниже, чем необходимо для отображения объекта с максимальным уровнем детализации;
• требуется быстро восстановить общие контуры объекта (без деталей), например, при поиске объекта в некоторой базе данных;
• в трехмерной сцене требуется изобразить объект “удаленным” на “значительной расстояние”.

Постепенная передача данных (Progressive Transmission). Задача состоит в следующем: организовать хранение данных, например, в файле так, чтобы уровень детализации объекта можно было бы увеличивать по мере постепенного считывания файла. Такой способ организации файла привлекателен, например, для передачи по сети: визуализацию объекта можно начинать еще до того, как закончилась пересылка всего файла. Этот же формат хорошо использовать для хранения объектов в базах данных для возможности быстрого просмотра (см. выше). Очевидно, что имея многомасштабное представления для объекта, такой формат несложно реализовать.

Редактирование объектов. Здесь используются те же идеи, что и для редактирования кривых.

1. Eric J. Stollnitz, Tony DeRose, David H. Salesin. Wavelets for Computer Graphics. Theory and Applications. Morgan Kaufmann Publishers, Inc., San Francisco, California, 1996, pp. 141-167.
2. M.H. Gross, O.G. Staadt, R. Gatti. Efficient Triangular Surface Approximations Using Wavelets and Quadtree Data Structures. IEEE Transactions on Visualization and Computer Graphics. Vol. 2, No. 2, June 1996.
3. Matthias Eck, Tony DeRose, Tom Duchamp, Hugues Hoppe, Michael Lounsbery, Werner Stuetzle. Multiresolution Analysis of Arbitrary Meshes. In SIGGRAPH’95 Conference, pp. 173-182. ACM, New York, 1995.
4. Michael Lounsbery, Tony DeRose, Joe Warren. Multiresolution Analysis for Surfaces of Arbitrary Topological Type. ACM Transactions on Graphics, Vol. 16, No. 1, January 1997, pp. 34-73.