
|
В 1671 году Джеймс Грегори установил, что:
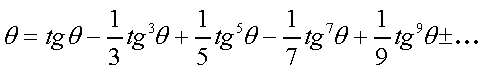
Этот результат позволил
Лейбницу получить очень простое выражение для PI, а именно:
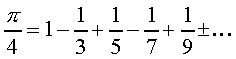
или, после умножения на 4:
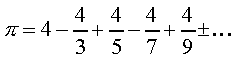
Просуммируйте этот ряд
и Вы получите число PI.
Однако, как говорил Козьма
Прутков, 'нельзя объять необъятное', что, в применении к данному
случаю, можно перефразировать так: нельзя просуммировать бесконечное
число слагаемых за конечное время, каким бы быстрым компьютером
мы не располагали.
Слава Богу, этого и не
требуется. Поскольку мы хотим найти не точное значение PI, а лишь
его приближение с пятью верными десятичными знаками, нам достаточно
просуммировать такое количество первых членов ряда, чтобы сумма
всех оставшихся членов не превышала 10-5.
Остался, правда, открытым
вопрос о том, сколько же все-таки членов ряда нужно просуммировать,
чтобы получить результат с требуемой точностью?
Ответ на этот вопрос в
'общем виде' выходит далеко за рамки настоящего обсуждения. Это
отдельная тема в курсах математического анализа и численных методов.
К счастью, данный конкретный
ряд позволяет найти очень простое правило, позволяющее определить
момент, когда следует прекратить суммирование. Дело в том, что
ряд Грегори является знакопеременным и сходится равномерно (хотя
и медленнее, чем хотелось бы). Это означает, что для любого нечетного
n, сумма первых n членов ряда всегда дает верхнюю
оценку для PI, а сумма n+1 первых членов ряда - нижнюю.
Значит, как только разница
между верхней и нижней оценками окажется меньше, чем требуемая
точность, можно смело прекращать вычисления и быть уверенным,
что как та, так и другая оценки отличаются от истинного значения
PI не более, чем на 10-5. В качестве окончательного результата
разумно взять среднее значение между полученными верхней и нижней
оценками.
Таким образом, можно предложить
алгоритм, приведенный ниже.
Положить n=0, S1 = 0 и S2 = 0; ( начальные установки )
Увеличить n на 1; ( n становится нечетным )
Вычислить S1 = S2 + 4/(2n-1); (S1 - есть верхняя оценка )
Увеличить n на 1; ( n становится четным )
Вычислить S2 = S1 - 4/(2n-1); (S2 - есть нижняя оценка)
Если S1 - S2 >= 10^(-5) перейти к шагу 2;
( нужная точность еще не достигнута )
Напечатать результат (S1 + S2) / 2
При реализации этого алгоритма
на машине следует помнить, что ряд Грегори сходится достаточно
медленно, и поэтому n может принимать довольно большие значения.
|

|
Для вычисления сколько-нибудь большого количества знаков пи предыдущий способ уже не годится. Но существует большое количество последовательностей, сходящихся к Пи гораздо быстрее. Воспользуемся, например, формулой Гаусса:
| p |
= 12arctan |
1 |
+ 8arctan |
1 |
- 5arctan |
1 |
|
|
|
|
| 4 |
18 |
57 |
239 |
Доказательство этой формулы несложное, поэтому мы его опустим.
Исходник программы, включающий в себя 'длинную арифметику'
Программа вычисляет NbDigits первых цифр числа Пи. Функция вычисления arctan названа arccot, так как arctan(1/p) = arccot(p), но расчет происходит по формуле Тейлора именно для арктангенса, а именно arctan(x) = x - x3/3 + x5/5 - ... x=1/p, значит arccot(x) = 1/p - 1 / p3 / 3 + ... Вычисления происходят рекурсивно: предыдущий элемент суммы делится и дает следующий.
/*
** Pascal Sebah : September 1999
**
** Subject:
**
** A very easy program to compute Pi with many digits.
** No optimisations, no tricks, just a basic program to learn how
** to compute in multiprecision.
**
** Formulae:
**
** Pi/4 = arctan(1/2)+arctan(1/3) (Hutton 1)
** Pi/4 = 2*arctan(1/3)+arctan(1/7) (Hutton 2)
** Pi/4 = 4*arctan(1/5)-arctan(1/239) (Machin)
** Pi/4 = 12*arctan(1/18)+8*arctan(1/57)-5*arctan(1/239) (Gauss)
**
** with arctan(x) = x - x^3/3 + x^5/5 - ...
**
** The Lehmer's measure is the sum of the inverse of the decimal
** logarithm of the pk in the arctan(1/pk). The more the measure
** is small, the more the formula is efficient.
** For example, with Machin's formula:
**
** E = 1/log10(5)+1/log10(239) = 1.852
**
** Data:
**
** A big real (or multiprecision real) is defined in base B as:
** X = x(0) + x(1)/B^1 + ... + x(n-1)/B^(n-1)
** where 0<=x(i)<B
**
** Results: (PentiumII, 450Mhz)
**
** Formula : Hutton 1 Hutton 2 Machin Gauss
** Lehmer's measure: 5.418 3.280 1.852 1.786
**
** 1000 decimals: 0.2s 0.1s 0.06s 0.06s
** 10000 decimals: 19.0s 11.4s 6.7s 6.4s
** 100000 decimals: 1891.0s 1144.0s 785.0s 622.0s
**
** With a little work it's possible to reduce those computation
** times by a factor 3 and more:
**
** => Work with double instead of long and the base B can
** be choosen as 10^8
** => During the iterations the numbers you add are smaller
** and smaller, take this in account in the +, *, /
** => In the division of y=x/d, you may precompute 1/d and
** avoid multiplications in the loop (only with doubles)
** => MaxDiv may be increased to more than 3000 with doubles
** => ...
*/
#include <time.h>
#include <stdio.h>
#include <malloc.h>
#include <math.h>
long B=10000; /* Working base */
long LB=4; /* Log10(base) */
long MaxDiv=450; /* about sqrt(2^31/B) */
/*
** Set the big real x to the small integer Integer
*/
void SetToInteger (long n, long *x, long Integer) {
long i;
for (i=1; i<n; i++) x[i] = 0;
x[0] = Integer;
}
/*
** Is the big real x equal to zero ?
*/
long IsZero (long n, long *x) {
long i;
for (i=0; i<n; i++)
if (x[i]) return 0;
return 1;
}
/*
** Addition of big reals : x += y
** Like school addition with carry management
*/
void Add (long n, long *x, long *y) {
long carry=0, i;
for (i=n-1; i>=0; i--) {
x[i] += y[i]+carry;
if (x[i]<B) carry = 0;
else {
carry = 1;
x[i] -= B;
}
}
}
/*
** Substraction of big reals : x -= y
** Like school substraction with carry management
** x must be greater than y
*/
void Sub (long n, long *x, long *y) {
long i;
for (i=n-1; i>=0; i--) {
x[i] -= y[i];
if (x[i]<0) {
if (i) {
x[i] += B;
x[i-1]--;
}
}
}
}
/*
** Multiplication of the big real x by the integer q
** x = x*q.
** Like school multiplication with carry management
*/
void Mul (long n, long *x, long q) {
long carry=0, xi, i;
for (i=n-1; i>=0; i--) {
xi = x[i]*q;
xi += carry;
if (xi>=B) {
carry = xi/B;
xi -= (carry*B);
}
else
carry = 0;
x[i] = xi;
}
}
/*
** Division of the big real x by the integer d
** The result is y=x/d.
** Like school division with carry management
** d is limited to MaxDiv*MaxDiv.
*/
void Div (long n, long *x, long d, long *y) {
long carry=0, xi, q, i;
for (i=0; i<n; i++) {
xi = x[i]+carry*B;
q = xi/d;
carry = xi-q*d;
y[i] = q;
}
}
/*
** Find the arc cotangent of the integer p (that is arctan (1/p))
** Result in the big real x (size n)
** buf1 and buf2 are two buffers of size n
*/
void arccot (long p, long n, long *x, long *buf1, long *buf2) {
long p2=p*p, k=3, sign=0;
long *uk=buf1, *vk=buf2;
SetToInteger (n, x, 0);
SetToInteger (n, uk, 1); /* uk = 1/p */
Div (n, uk, p, uk);
Add (n, x, uk); /* x = uk */
while (!IsZero(n, uk)) {
if (p<MaxDiv)
Div (n, uk, p2, uk); /* One step for small p */
else {
Div (n, uk, p, uk); /* Two steps for large p (see division) */
Div (n, uk, p, uk);
}
/* uk = u(k-1)/(p^2) */
Div (n, uk, k, vk); /* vk = uk/k */
if (sign) Add (n, x, vk); /* x = x+vk */
else Sub (n, x, vk); /* x = x-vk */
k+=2;
sign = 1-sign;
}
}
/*
** Print the big real x
*/
void Print (long n, long *x) {
long i;
printf ("%d.", x[0]);
for (i=1; i<n; i++) {
printf ("%.4d", x[i]);
if (i%25==0) printf ("%8d\n", i*4);
}
printf ("\n");
}
/*
** Computation of the constant Pi with arctan relations
*/
void main () {
clock_t endclock, startclock;
long NbDigits=10000, NbArctan;
long p[10], m[10];
long size=1+NbDigits/LB, i;
long *Pi = (long *)malloc(size*sizeof(long));
long *arctan = (long *)malloc(size*sizeof(long));
long *buffer1 = (long *)malloc(size*sizeof(long));
long *buffer2 = (long *)malloc(size*sizeof(long));
startclock = clock();
/*
** Formula used:
**
** Pi/4 = 12*arctan(1/18)+8*arctan(1/57)-5*arctan(1/239) (Gauss)
*/
NbArctan = 3;
m[0] = 12; m[1] = 8; m[2] = -5;
p[0] = 18; p[1] = 57; p[2] = 239;
SetToInteger (size, Pi, 0);
/*
** Computation of Pi/4 = Sum(i) [m[i]*arctan(1/p[i])]
*/
for (i=0; i<NbArctan; i++) {
arccot (p[i], size, arctan, buffer1, buffer2);
Mul (size, arctan, abs(m[i]));
if (m[i]>0) Add (size, Pi, arctan);
else Sub (size, Pi, arctan);
}
Mul (size, Pi, 4);
endclock = clock ();
Print (size, Pi); /* Print out of Pi */
printf ("Computation time is : %9.2f seconds\n",
(float)(endclock-startclock)/(float)CLOCKS_PER_SEC );
free (Pi);
free (arctan);
free (buffer1);
free (buffer2);
}
Конечно, это не самые эффективные способы вычисления числа пи. Существует еще громадное количество
формул. Например, формула Чудновского (Chudnovsky), разновидности которой используются в Maple. Однако в обычной практике программирования формулы Гаусса вполне хватает,
поэтому эти методы не будут описываться в статье. Вряд ли кто-то хочет вычислять миллиарды знаков пи, для которых
сложная формула дает большое увеличение скорости.
|