Под принадлежностью точки многоугольнику принимается принадлежность точки внутренности многоугольника или его границе. В частности, все вершины принадлежат многоугольнику.

Для треугольника существует стандартный алгоритм, который надо знать, хотя и более общий тоже годится. Это - 'классика' аналитической геометрии, и в ручных расчетах используется именно он.

Функция pointInTriangle проверяет точки на попадание внутрь треугольника: функция возвращает значение TRUE, если точка р находится внутри треугольника а, b и с, в противном случае возвращаемое значение равно FALSE. Используемая функция classify определяет положение точки p относительно прямой, задаваемой аргументами. Ее описание можно прочитать в разделе 'Структуры геометрических данных'.

bool pointInTriangle (Point p, Point a, Point b, Point c)
{
  return ((p.classify (a, b) != LEFT) &&
        (p.classify(b, c) != LEFT) &&
        (p.classify(c, a) != LEFT));
}

В том же разделе описана функция для произвольного выпуклого многоугольника. Проверяется тот факт, что точка лежит по одну сторону от всех ребер полигона. Если это не так, то она снаружи. В общем случае такой способ не работает.

По книге Ласло,
"Вычислительная геометрия и компьютерная графика на С++"

Предположим, что нам необходимо определить принадлежность точки а полигону р. Для этого из некоторой удаленной точки проведем прямую линию в точку а. На этом пути может встретиться нуль или несколько пересечений границы полигона: при первом пересечении мы входим внутрь полигона, при втором — выходим из него, при третьем пересечении снова входим внутрь и так до тех пор, пока не достигнем точки а. Таким образом каждое нечетное пересечение означает попадание внутрь полигона р, а каждое четное — выход из него. Если мы попадаем в точку а с нечетным числом пересечений границы полигона, то точка а лежит внутри полигона, а если получается четное число пересечений, то точка находится вне полигона р. Например, на рис. 1 луч r_a пересекает границу только однажды, поскольку единица число нечетное, то точка а находится внутри полигона. Относительно точки b мы прийдем к заключению, что она лежит вне полигона, поскольку луч r_b пересекает границу четное число раз (дважды).

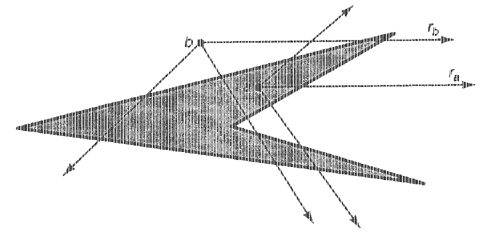
Построение алгоритма на основе этой идеи базируется на двух особенностях. Во-первых, для решения задачи подходит любой луч, начинающийся в анализируемой точке а (рис. 1). Поэтому для прпстоты выберем правый горизонтальный луч r_a, начинающийся в точке а и направленный вправо параллельно положительной полуоси х.

Во-вторых, порядок расположения ребер, пересекаемых лучом r_a безразличен, имеет значение лишь парность (четное или нечетное количество) их общего числа. Следовательно, вместо моделирования движения вдоль луча r_a для алгоритма достаточно определить все пересечения ребер в любом порядке, определяя четность по мере продвижения. Простейшим решением будет обход границы полигона с переключением бита четности при каждом обнаружении ребра, пересекаемого лучом r_a.

Относительно горизонтального луча r_a, направленного вправо, будем различать три типа ребер полигона: касательное ребро, содержащее точку а; пересекающее ребро, не содержащее точку а; безразличное ребро, которое совсем не имеет пересечения с лучом га. Например, на рис. 2 ребро с является пересекающим ребром, ребро d — касательным, а ребро е — безразличным.

Функция pointlnPolygon решает задачу о принадлежности для точки а и полигона р. В процессе работы алгоритма обходится граница полигона и переключается переменная parity для каждого обнаруженного факта пересечения ребра лучом. Возвращается значение INSIDE типа перечисления, если окончательное значение переменной parity равно 1 (означающее нечетное число), или возвращает OUTSIDE, если это конечное значение равно О (означающее четность). Если обнаруживается касательное ребро, то алгоритм немедленно возвращает значение типа перечисления BOUNDARY (граница). Реализация использует классы из раздела 'Структуры геометрических данных'.

enum { INSIDE, OUTSIDE, BOUNDARY };         // положение точки
//     ВНУТРИ, ВНЕ,     НА ГРАНИЦЕ
enum { TOUCHING, CROSSING, INESSENTIAL };   // положение ребра
//     КАСАТЕЛbНОЕ, ПЕРЕСЕКАЮЩЕЕ, НЕСУЩЕСТВЕННОЕ

int pointInPolygon(Point &a, Polygon &p)
{
  int parity = 0;
  for (int i = 0;  i < p.size(); i++, p.advance (CLOCKWISE)) { 
    Edge e = p.edge();
    switch (edgeType(a, e)) {
      case TOUCHING:
        return BOUNDARY;
      case CROSSING:
        parity = 1 - parity;
    }
  }
  return (parity ? INSIDE : OUTSIDE);
}

Обращение к функции edgeTypefa, e) классифицирует положение ребра е относительно горизонтального луча r_a, направленного вправо, возвращая значения TOUCHING, CROSSING или INESSENTIAL (касательное, пересекающее или безразличное) типа перечисления. Определение функции edgeType несколько хитроумное, поскольку функция pointInPolygon должна правильно обрабатывать особые ситуации, возникающие при прохождении луча га точно через вершины.

Рассмотрим рис. 3. В случае (а) бит четности должен быть переключен — луч пересекает границу только однажды, хотя при этом на самом деле пересекает два ребра. В случаях (б) и (в) четность не изменяется. Это может быть достигнуто путем некоторого уточнения схемы классификации ребер:

• Ребро е — касательное ребро, если оно содержит точку а.
• Ребро е — пересекающее ребро, если (1) ребро е не горизонтальное и (2) луч r_a пересекает ребро е в некоторой точке, отличающейся от его нижней конечной точки.
• Ребро е — безразличное, если оно не касательное и не пересекающее.
  
  Рис. 3:  Специальные случаи: (а) и (г) — переменная parity переключается однажды; (6) и (д) - parity не изменяется, (в) и (е) — parity переключается дважды и ситуация остается без изменения
  

  Обращаясь к рис. 3, мы можем видеть, что в случае (а) переменная parity должна переключиться однажды, в случае (б) parity не изменяется, в случае (в) parity переключается дважды и ситуация остается без изменения. Заметим, что горизонтальное ребро, не включающее точку а, считается безразличным и оно игнорируется функцией pointInPolygon. Поэтому случаи (г), (д) и (е) обрабатываются точно так же, как соответствующие случаи (а), (б) и (в).

  Итак, функция edgeType классифицирует ребро е как TOUCHING, CROSSING или INESSENTIAL (пересекающее, касательное или безразличное) относительно точки а:

  int edgeType (Point &a, Edge &e)
  {
    Point v = e.org;
    Point w = e.dest;
    switch (a.classify(e)) {
      case LEFT:
        return ((v.y<a.y)&&(a.y<=w.y)) ? CROSSING : INESSENTIAL; 
      case RIGHT:
        return ((w.y<a.y)&&(a.y<=v.y)) ? CROSSING : INESSENTIAL; 
      case BETWEEN:
      case ORIGIN:
      case DESTINATION:
        return TOUCHING;
      default:
        return INESSENTIAL;
    }
  }
  

  Обратите внимание, как функция edgeType обнаруживает пересекающие ребра. Если точка а лежит слева от ребра е, то ребро является пересекающим, только если вершина начала ребра v(=e.org) лежит ниже луча r_a, а вершина конца w(=e.dest) расположена на луче или лежит выше его. Тогда ребро не может быть горизонтальным и луч га должен пересекать ребро в некоторой точке, отличающейся от его нижнего конца. Если точка а находится справа от ребра е, то роли конечных точек v и w взаимно меняются.

  В худшем случае (когда точка а не принадлежит границе полигона) время выполнения программы pointInPolygon пропорционально размеру полигона.