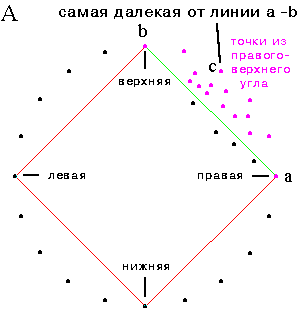
Этот алгоритм начинает работу с создания четырехугольника, соединяющего крайние точки ( смотри шаг А ). Только точки, лежащие вне его могут лежать на оболочке и будут рассматриваться в дальнейшем. Каждый лежащий вне четырехугольника участок будет рекурсивно обработан функцией Quickhull. На диаграмме ниже изображена обработка верхнего-правого угла.

На шаге А также находится точка точка с, наиболее удаленная от линии ( a , b ). Следующим шагом мы определяем два множества точек: cправа или на линии ( a , c ) и справа или на ( c , b ). Для них вновь запускаем функцию Quickhull.

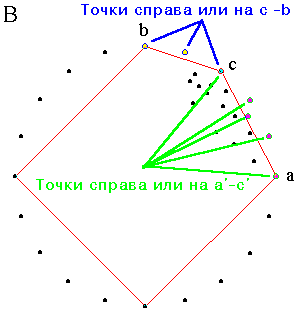
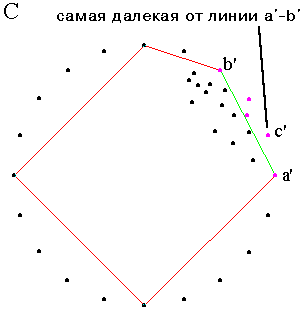
Ниже изображена аналогичная обработка первого множества. Находится точка c' ( cм. С ), наиболее удаленная от линии (a',b'), определяются два новых множества точек: справа или на (a',c') и (c',b')... Получается D, которое обрабатывается дальше..

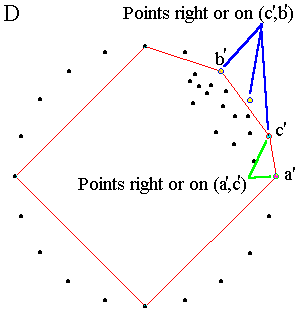
Алгоритм продолжает вызывать Quickhull для этих двух множеств. На рис. E и F показан результат вызова для первого множества. Если множество состоит только из двух точек, рекурсия останавливается, возвращая эти две точки как сторону выпуклой оболочки ( Шаг F, сторону изображает черная линия ).

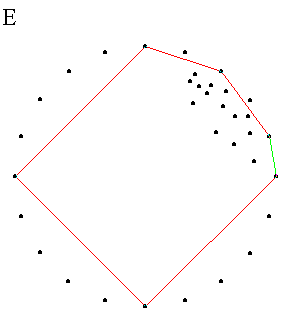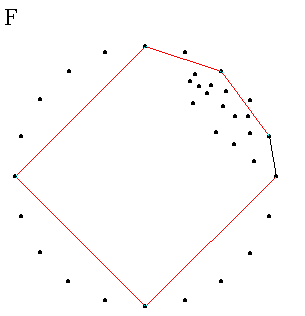
Затем обрабатывается второе множество ( Шаг G ), и опять рекурсия останавливается, добравшись до двух точек. И так продолжается, пока не обработан весь верхний-правый угол. После этого ( Шаг H )у нас готова выпуклая оболочка для этого региона.

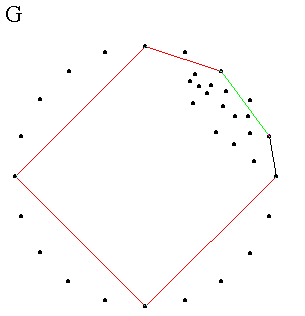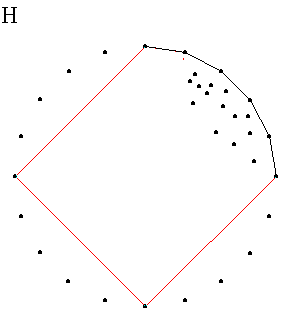
Аналогичным способом обрабатываются верхний-левый, нижний-левый и нижний-правый углы, пока не получим полную выпуклую оболочку ( Шаг I ).

Наихудшее поведение алгоритм демонстрирует в случае, если заданные точки уже образуют выпуклый многоугольник, так как никакие точки в этом случае не отбрасываются. Тогда он делает Theta(n²) операций.

Находим самую левую и самую правую точки. 
Запускаем Quickhull для множества точек выше соединяющего их отрезка и ниже.

function QuickHull(a,b,s) {
  if S={a,b} then return(a,b)
  else {
    c = index of right of (a,c)
    A = точки справа от (a,c)
    B = точки справа от (a,b)
    return QuickHull(a,c,A) объединенное с QuickHull(c,b,B)
}

Исходник на Си

#include <stdlib.h>
#include <math.h>

#define N 3              /* the number of points */

int pt[N], belongs_to_hull[N], *upper, *lower;

/* x and y point coordinates */
double x[N], y[N];

/* the result vector; indicates whether a point belongs to the hull*/
int belongs_to_hull[N];


/* output routines: */
void print_array( int *pt, int n )
{
  long j;

  printf("Array with %d points:\n", n );
  for (j=0; j<n; j++)
    printf("point %d = (%d,%d)\n", pt[j], (int)x[pt[j]], (int)y[pt[j]] );
  printf("\n");
}

void print_hull( void )
{
  int j;

  printf("Points of the convex hull:\n");
  for (j=0; j<N; j++)
    if (belongs_to_hull[j]) 
      printf(" (%d,%d)", (int)x[j], (int)y[j] );
}


/* quickhull algorithm, applied to set S of n points (x[],y[]) */

#define cross(p,a,b) \
 /* return crossproduct of vectors p-a and b-a */ \
 ((x[a]-x[p])*(y[b]-y[p]) - (y[a]-y[p])*(x[b]-x[p]))

#define leftturn(a,b,c) \
 /*true iff point c is lefthand of vector through points (a,b) */ \
 (cross(c,a,b)>0.0)

int *delete_right( int *pt, int *num, int p1, int p2 )
{
  int j;
  int leftcnt;
  int *left;
  int n = *num;

  /* delete all points in pt located right from line p1p2: */
  left = (int *) malloc( n * sizeof(int) );
  left[0]=p1; left[1]=p2;
  leftcnt = 2;
  for (j=0; j<*num; j++)
    if (!(pt[j]==p1 || pt[j]==p2))   /*p1 and p2 already in left[]*/
      if (leftturn(p1,p2,pt[j])) /* point j is lefthand to vector p1p2 */
        left[leftcnt++] = pt[j];

  *num = leftcnt;
  return left;
}


void inithull( int *pt, int n, int *minx, int *maxx )
{
  int p1, p2;
  int i;

  /* determine points p1,p2 with minimal and maximal x coordinate: */
  p1 = p2 = pt[0];   /* init. p1,p2 to first point */
  for (i=1; i<n; i++) {   /* seq. search for minimum / maximum */
    if (x[pt[i]] < x[p1])   p1 = i;
    if (x[pt[i]] > x[p2])   p2 = i;
  }
  belongs_to_hull[p1] = 1;
  belongs_to_hull[p2] = 1;
  *minx = p1; *maxx = p2;
}


int pivotize( int *pt, int n )    /* n>=3 is assumed */
  /* as pivot, select the point in pt[]-{p1,p2} with maximal
   * cross_prod( pivot-p1, p2-p1 )
   */
{
  int i, p1=pt[0], p2=pt[1];
  int pivotpos = 2;
  double maxcross = cross(pt[2], p1, p2);
  for (i=3; i<n; i++) {        /* sequential maximization */
    double newcross = cross(pt[i], p1, p2);
    if (newcross > maxcross) {
      maxcross = newcross;
      pivotpos = i;
    }
  }
  return pt[pivotpos];
}


void qh( int *pt, int n )
{
  /* DC step: select pivot point from pt */
  int pivotpos, pivot;
  int p1=pt[0], p2=pt[1];
  int *left1, *left2, leftcnt1, leftcnt2;

  /* DC step: select any pivot point from pt.
     We have p1==pt[0],p2==pt[1] */
  if (n==2) return;

  if (n==3) { 
    /* one point (beyond old p1,p2) must belong to hull */
    belongs_to_hull[pt[2]] = 1;      /* saves a recursive call */
    return;
  }

  pivot = pivotize( pt, n );

  belongs_to_hull[pivot] = 1;
  leftcnt1 = n;

  left1 = delete_right( pt, &leftcnt1, p1, pivot );

  qh( left1, leftcnt1 );
  leftcnt2 = n;

  left2 = delete_right( pt, &leftcnt2, pivot, p2 );
  qh( left2, leftcnt2 );
}


int main( void )
{

  int uppercnt, lowercnt;
  int j;  
  int minxpt, maxxpt;
  double xj;
     
  for (j=0; j<N; j++) {
    x[j] = rand();
    y[j] = rand();
    pt[j] = j;
  }

  print_array(pt, N);

  upper = (int *)malloc(N*sizeof(int));
  lower = (int *)malloc(N*sizeof(int));

  /* random points initialization */
  for (j=0; j<N; j++) belongs_to_hull[j] = 0;   

  inithull( pt, N, &minxpt, &maxxpt );

  /*  now split original set of points:
   *  into upper[] (all nodes left of (p1,p2), including p1,p2
   *  and  lower[] (all points right of (p1,p2), including p1,p2
  */
 
  uppercnt = lowercnt = N;

  upper = delete_right( pt, &uppercnt, minxpt, maxxpt );
  lower = delete_right( pt, &lowercnt, maxxpt, minxpt );

  qh( upper, uppercnt );
  qh( lower, lowercnt );

  print_hull();

  return 1;
}