Проведем через пары точек две прямые. Первая линия пусть проходит через
P1 и P2, а прямая b - через
P2 и P3.
Уравнения этих прямых будут

где m - коэффициент наклона линии, получаемый из
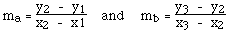
Центр круга - находится на пересечении двух перпендикулярных прямых, проходящих через середины отрезков
P1P2 и
P2 P3.
Легко доказать, что прямая, перпендикулярная к линии с коэффициентом наклона m имеет
коэффициент наклона -1/m, значит уравнения прямых, перпендикулярных a и b
и проходящих через середины
P1P2 и
P2P3 будут
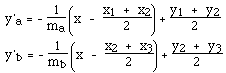
Они пересекаются в центре, и решение относительно x дает
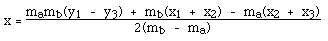
Значение у вычислим подстановкой x в уравнение одного из перпендикуляров.
Можно и наоборот: сначала решить относительно y, а потом найти x.
|