
|
Стандартное уравнение плоскости -
Ax + By + Cz + D = 0
Вектор (A, B, C) перпендикулярен плоскости.
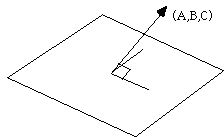
Уравнение плоскости по трем точкам
(x1,y1,z1),
(x2,y2,z2),
(x3,y3,z3) можно получить из следующих опрееделителей:
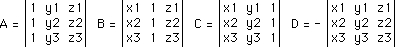
Раскрывая, получаем
A = y1 (z2 - z3) + y2 (z3 - z1) + y3
(z1 - z2)
B = z1 (x2 - x3) + z2 (x3 - x1) + z3
(x1 - x2)
C = x1 (y2 - y3) + x2 (y3 - y1) + x3
(y1 - y2)
- D = x1
(y2 z3 - y3 z2) +
x2 (y3 z1 - y1 z3) +
x3 (y1 z2 - y2 z1)
Следует заметить, что, если все точки лежат на одной прямой, то (A,B,C) будет (0,0,0).
Знак s = Ax + By + Cz + D определяет, с какой стороны по отношению к плоскости находится точка (x,y,z). Если s > 0, то точка лежит в той стороне, куда указывает нормальный вектор (A,B,C). Если s < 0 - на противаположной стороне, а в случае s = 0 точка принадлежит плоскости.
|

|
Если вектор N перпендикулярен плоскости, то все принадлежащие ей точки p удовлетворяют равенству
N . p = k
где . - скалярное произведение двух векторов.
т.е: a . b =
(ax,ay,az) .
(bx,by,bz) =
ax bx + ay by + az
bz
Если точка a принадлежит плоскости, то
N *(p - a) = 0
|