
|
Рассмотрим проблему вычисления области пересечения Р П Q двух выпуклых полигонов Р и Q. За исключением особо оговоренных случаев будем предполагать, что два полигона пересекаются невырожденно: пересечение двух ребер происходит в одной единственной точке, не являющейся вершиной какого-либо полигона. Учитывая такое предположение о невырожденности, всегда получим, что полигон Р П Q состоит из попеременных цепочек из Р и Q. Каждая пара последовательных цепочек соединяется в точке пересечения, в которой пересекаются границы полигонов Р и Q (рис. 1).
Рис. 1: Структура полигона пересечения Р П Q
Существует несколько решений этой задачи с линейной зависимостью времени выполнения от суммарного числа вершин. Описываемый здесь алгоритм обладает особым изяществом и его легко применять. Для двух заданных на входе выпуклых полигонов Р и Q алгоритм определяет окно на ребре полигона Р и еще одно окно на ребре полигона Q. Идея заключается в продвижении этих окон вдоль границ полигона по мере формирования полигона пересечения Р П Q: окна как бы проталкивают друг друга вдоль границы своих соответствующих полигонов в направлении по часовой стрелке для поиска точек пересечения ребер. Поскольку точки пересечения обнаруживаются в том порядке, в котором они располагаются вокруг полигона Р П Q, полигон пересечения оказывается сформированным, когда некоторая точка пересечения будет обнаружена вторично. В противном случае, если не будет обнаружено ни одной точки пересечения после достаточного числа итераций, то значит границы полигонов не пересекаются. В этом случае потребуется дополнительный простой тест, не содержится ли один полигон внутри другого или они вовсе не пересекаются.
Для объяснения работы оказывается весьма полезным ввести понятие серпа. На рис. 2 серпами будут шесть затененных полигонов. Каждый из них ограничен цепочкой, взятой от полигона Р, и цепочкой от полигона Q, ограниченных двумя последовательными точками пересечения. Внутренней цепочкой серпа будет та часть, которая принадлежит полигону пересечения. Отметим, что полигон пересечения окружен четным числом серпов, внутренние цепочки которых попеременно являются частями границ полигонов Р и Q.
Рис. 2: Серпы, окружающие полигон пересечения
В терминах серпов алгоритм поиска полигона пересечения проходит две азы. В процессе первой фазы окно р полигона Р и окно q полигона Q перевещаются в направлении по движению часовой стрелки до тех пор, пока они не будут установлены на ребрах, принадлежащих одновременно одному тому же серпу. Каждое окно начинает свое движение с произвольной позиции. Здесь для краткости будем использовать один и тот же символ р для обозначения как окна полигона Р, так и ребра в этом окне. Тогда термин "начало р" будет относиться к точке начала ребра в окне полигона P, команда "продвинуть р" будет означать, что необходимо переместить окно полигона Р на следующее ребро. Аналогичным образом буквой q будем обозначать как окно полигона Q, так и ребро в окне. Иногда ребра р и q будем читать текущими ребрами.
Во время фазы 2 р и q продолжают перемещаться в направлении по ча-эвой стрелке, но на этот раз они двигаются в унисон от одного серпа к еднему серпу. Перед тем как любое окно перейдет из текущего серпа в седний, ребра р и q пересекутся в точке пересечения, соединяющей оба ерпа. Полигон пересечения строится именно во время второй фазы. Перед каждым перемещением р конечная точка ребра р заносится в полигон перечения, если ребро р принадлежит внутренней цепочке текущего серпа Аналогичным образом перед перемещением q фиксируется конечная точка ребра q, если q принадлежит внутренней цепочке текущего серпа. При кая дом пересечении ребер р и q точка пересечения, в которой они пересекаются, записывается в полигон пересечения.
Для принятия решения, какое из окон должно перемещаться, в алгоря ме используется правило перемещения. Это правило основано на следующв замечаниях: говорят, что ребро а нацелено на ребро b, если бесконечная прямая линия, определяемая ребром b, расположена перед а (рис. 3)
Рис. 3: Только показанные толстыми линиями ребра нацелены на ребро q, остальные - нет
Ребро а нацелено на b, если выполняется одно из условий:
- а х b > 0 и точка a.dest не лежат справа от b или
- а х b < 0 и точка a.dest не лежат слева от b.
Заметим, что соотношение а х b >= 0 соответствует случаю, при котором угол между векторами a и b меньше 180 градусов
Функция aimsAt возвращает значение TRUE, если и только если ребр а нацелено на ребро b. Параметр aclass указывает на положение конечно точки a.dest относительно ребра b.
Параметр crossType принимает значение COLLINEAR, если и только если ребра а и b коллинеарны. Реализация использует классы из раздела структуры геометрических данных
bool aimsAt (Edge &a, Edge &b, int aclass, int crossType)
{
Point va = a.dest - a.org;
Point vb = b.dest - b.org;
if (crossType != COLLINEAR) {
if ( (va.x * vb.y) >= (vb.x * va.y) )
return (aclass != RIGHT);
else
return (aclass != LEFT);
} else {
return (aclass != BEYOND);
}
}
Если ребра а и b коллинеарны, то ребро а нацелено на b, если конечна точка a.dest не лежит после b. Это обстоятельство используется для тоге чтобы продвинуть а вместо b, когда два ребра пересекаются вырожденно более, чем в одной точке. Позволяя а "догонять" b, мы обеспечиваем, что ни одна точка пересечения не будет пропущена.
Возвратимся к обсуждению правил перемещения. Они сформулированы таким образом, чтобы не пропустить следующую точку пересечения. Правила отличают текущее ребро, которое может содержать следующую точку пересечения, от текущего ребра, которое возможно не может содержать следующей точки пересечения, причем в этом случае окно переносится вполне безопасно. Правила перемещения различают четыре ситуации, показанные на рис. 4. Здесь ребро а считается находящимся вне ребра b, если конечная точка a.dest расположена слева от b.
Рис. 4: Четыре правила перемещения: (а)-продвинуть р; б - продвинуть р,- в — продвинуть р; г — продвинуть р
- р и q нацелены друг на друга: перемещается окно, соответствующее тому ребру (р или q), которое находится снаружи другого. В ситуации рис. 4а должно быть перенесено окно на ребре р. Следующая точка пересечения не может лежать на р, поскольку ребро р находится вне полигона пересечения.
- р нацелено на q, но q не нацелено на р: конечная концевая точка ребра р заносится в полигон пересечения, если р не находится снаружи q и затем окно р переносится. На рис. 46 ребро р не может содержать следующей точки пересечения (хотя оно может содержать некоторую точку пересечения, если р находится не снаружи от q). На рис. показана ситуация, в которой ребро р, окно которого должно быть перенесено, не находится снаружи от ребра q.
- q нацелено на р, но р не нацелено на q: конечная концевая точка ребра q заносится в полигон пересечения, если q не находится снаружи от р, после чего переносится окно q (рис. 6.14в). Этот случай симметричен предыдущему. На рис. показана ситуация, при которой ребро q, окно которого должно быть перенесено, находится снаружи от ребра Р-
- р и q не нацелены друг на друга: переносится то окно, которое относится к ребру, расположенному снаружи от другого. Согласно рис. 4 необходимо перенести окно р, поскольку ребро р находится снаружи от ребра q.
Работа алгоритма показана на рис. 5. Каждое ребро имеет метку i, если оно обрабатывается на шаге i (у некоторых ребер показана двойная метка, поскольку они обрабатываются дважды). Два начальных ребра имеют метку 0. На этом рисунке фаза 2 (когда два текущих ребра оказывал принадлежащими одному и тому же серпу) начинается после трех итераций
Рис. 5: Поиск полигона пересечения. Для ребра указана метка i, если оно обрабатывается на шаге i. Два начальных ребра обозначены меткой О
Алгоритм реализован в программе convexPolygonlntersect. Програ передаются полигоны Р и Q, она возвращает указатель на резулътирукя полигон пересечения R. Обращение к функции advance использовано переноса одного из двух текущих ребер и для включения конечной конце вой точки ребра в полигон R в соответствии с выполнением определеннь условий. Используются окна, существующие внутри класса Polygon.
enum ( UNKNOWN, P_IS_INSIDE, Q_IS_INSIDE);
Polygon *convexPolygonlntersect(Polygon &P, Polygon &Q)
{
Polygon *R;
Point iPnt, startPnt;
int inflag = UNKNOWN;
int phase = 1;
int maxItns = 2 * (P.size() + Q.size());
// начало цикла for
for (int i = 1; (i<=maxItns) || (phase==2); i++) {
Edge p = P.edge();
Edge q = Q.edge();
int pclass = p.dest.classify (q);
int qclass = q.dest.classify (p);
int crossType = crossingPoint (p, q, iPnt);
if (crossType = SKEW_CROSS) {
if (phase==1) {
phase = 2;
R = new Polygon;
R->insert(iPnt);
startPnt = iPnt;
} else if (iPnt != R->point() ) {
if (iPnt != startPnt)
R->insert(iPnt);
else
return R;
}
if (pclass==RIGHT) inflag = P_IS_INSIDE;
else if (qclass=RIGHT) inflag = Q_IS_INSIDE;
else inflag = UNKNOWN;
} else if ( (crossType—COLLINEAR) && (pclass != BEHIND) && (qclass ! = BEHIND) )
inflag = UNKNOWN;
bool pAIMSq = aimsAt(p, q, pclass, crossType);
bool qAIMSp = aimsAt(q, p, qclass, crossType);
if (pAIMSq && qAIMSp) {
if ( (inflag == Q_IS_INSIDE) || ( (inflag == UNKNOWN) && (pclass == LEFT)))
advance(P, *R, FALSE);
else
advance (Q, *R, FALSE);
} else if (pAIMSq) {
advance (P, *R, inflag == P_IS_INSIDE);
} else if (qAIMSp) {
advance (Q, *R, inflag == Q_IS_INSIDE);
} else {
if ((inflag == Q_IS_INSIDE) ((inflag == UNKNOWN) && (pclass == LEFT)))
advance ( P , *R , FALSE );
else
advance (Q, *R, FALSE);
}
}
// конец цикла for
if (pointInConvexPolygon ( P.point (), Q) )
return new Polygon (P);
else if (pointInConvexPolygon (Q.point(), P) )
return new Polygon(Q);
return new Polygon;
}
Если после выполнения 2(|Р| + |Q|) итераций не будет обнаружено ни одной точки пересечения, то основной цикл завершается, поскольку это означает, что границы полигона не пересекаются. Последующие обращения к функции pointlnConvexPolygon производятся с целью обнаружения ситуаций Р С Q, Q П Р или Р П Q = 0. В противном случае, если найдена некоторая точка пересечения iPnt, то алгоритм продолжает построение полигона пересечения R и останавливается только после того, как точка iPnt будет обнаружена вторично.
Переменная inflag показывает, какой из двух входных полигонов находится в данный момент внутри другого — т. е. указывает на полигон, текущее ребро которого находится в составе внутренней цепочки текущего серпа. Более того, переменная inflag принимает значение UNKNOWN (неизвестно) во время первой фазы, а также всякий раз, когда оба текущих ребра коллинеарны или перекрывают друг друга. Значение этой переменной меняется при каждом обнаружении новой точки пересечения.
Процедура advance продвигает текущее ребро полигона А, представляющее либо Р, либо Q. Эта же процедура заносит конечную концевую точку ребра х в полигон пересечения R, если А находится внутри другого полигона и * не была последней точкой, записанной в R:
void advance (Polygon &A, Polygon &R, int inside)
{
A. advance (CLOCKWISE);
if (inside && (R.point() != A.point ()))
R.insert (A.point());
}
|

|
Доказательство корректности показывает наиболее важные моменты ра боты алгоритма — один и тот же набор правил продвижения работает течение обеих фаз. Правило продвижения заносит р и q в один и тот на серп и затем передвигает р и q в унисон из одного серпа в другой.
Корректность алгоритма следует из двух утверждений:
- Если текущие ребра р к q принадлежат одному и тому же серпу, тогда можно будет найти следующую точку пересечения, в которой закаа чивается текущий серп, и эта точка будет именно следующей.
- Если границы полигонов Р и Q пересекаются, то текущие ребра р и пересекутся в некоторой точке пересечения после не более, чем 2(|Р| + |Q|) итераций.
Утверждение 2 обеспечивает, что алгоритм найдет некоторую точку пересечения, если таковая существует. Поскольку ребра р и q принадлежат одному и тому же серпу, если они пересекаются, то из утверждения 1 следует, что остальные точки пересечения будут найдены в нужном порядке.
Рассмотрим сначала утверждение 1. Предположим, что р и q принадлежат одному и тому же серпу и q достигает некоторой точки пересечения раньше, чем р. Мы покажем, что тогда q останется неподвижным, пока не достигнет точки пересечения после ряда последовательных продвижений Могут возникнуть две ситуации. Сначала предположим, что р нахрдится снаружи от q (рис. 6а). При этом q останется фиксированным, пока будет продвигаться согласно нулю или нескольким применениям правила 4 затем нулю или нескольким применениям правила 1 и потом нулю или нескольким применениям правила 2. Во второй ситуации предположим, что р не находится снаружи от q (рис. 66). Здесь q будет оставаться фиксированным, пока р будет продвигаться путем нуля или нескольких применений правила 2. В симметричной ситуации, когда р достигает точки пересечения раньше, чем q, ребро q остается фиксированным, а ребро q продвигается до точки встречи. Это можно показать аналогичным образом, только меняется роль р и q и правило 3 заменяет правило 2. Из этого следует утверждение 1.
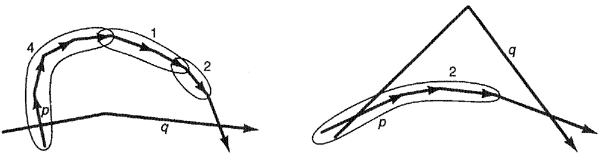 Рис. 6: Продвижение к следующей точке пересечения
Чтобы показать утверждение 2, предположим, что границы Р и Q пересекаются. После |Р| + |Q| итераций либо р, либо q должны совершить полный оборот вокруг своего полигона. Предположим, что это произошло с р. В некоторый момент времени ребро р должно расположиться так, что оно будет содержать точку пересечения, в которой полигон Q переходит извне полигона Р внутрь его. Это происходит потому, что существуют по крайней мере две точки пересечения и направление пересечения меняется. Пусть q будет ребром внутри окна полигона Q в момент обнаружения такого р.
На рис. 7 граница полигона Q разбита на две цепочки Сr и Cs. Первая цепочка Сr заканчивается в ребре qr, в том ребре полигона Q, которое входит внутрь полигона Р через его ребро р. Другая цепочка Cs заканчивается в ребре qs, конечная точка которого лежит справа от бесконечной прямой линии, определяемой ребром р, и она наиболее удалена от этой прямой линии. Следует рассмотреть два случая в зависимости от того, какой из двух цепочек принадлежит ребро q:
Рис. 7: Иллюстрация к доказательству, что можно найти точку пересечения, если границы Р и Q пересекаются
Случай 1 [q принадлежит Сr]. Здесь р остается фиксированным, тогда как q продвигается согласно нулю или нескольким применениям правила 3, затем правила 4, потом правила 1 и, наконец, правила 3, когда обнаруживается точка пересечения.
Случай 2 [qi принадлежит Сr]. Здесь q остается фиксированным, а р продвигается согласно нулю или нескольких применений правила 2, затем правила 4, потом оравила 1 и, наконец, правила 2 в момент, когда р окажется внутри q. С этого момента оба ребра р и q могут продвигаться несколько раз, однако ребро q не может быть продвинуто за его следующую точку пересечения, пока р сначала не достигнет предыдущей точки пересечения ребра q (если этого уже не произошло с ребром р). Поскольку р и q заканчиваются в одном и том же серпе, утверждение 1 гарантирует, что после некоторого числа дополнительных продвижений они пересекутся в точке пересечения, в которой заканчивается текущий серп.
Чтобы показать, что достаточно 2(|Р| + |Q|) итераций для поиска некоторой точки пересечения, заметим, что при доказательстве утверждения 2 (о том, что граница полигона Q входит внутрь полигона Р через ребро р при произвольном положении ребрв q) начальные позиции р и q достигались при выполнении не более |Р| + |Q| итераций. Фактически такая ситуация, либо симметричная ей, в оторой роли р и q взаимно заменяются, достигается за меньшее число итераций. Поскольку после этого ни р, ни q не будут продвинуты на полный оборот прежде, чем будет достигнута первая точка пересечения, потребуется не более |Р| + |Q| дополнительных продвижений.
|

|
Наш алгоритм определения пересечения двух выпуклых полигонов очеш чувствителен к ошибкам округления, когда два полигона пересекаются i точке, являющейся вершиной одного или обоих полигонов. Одна из проблем заключается в том, что такая точка может быть пропущена. В одном ш случаев на рис.3 ребра р и q пересекаются в точке х, являющейся ко нечной концевой точкой ребра р. При использовании точной арифметики параметрическое значение х вдоль отрезка р равно единице. Однако в арифметике с плавающей точкой фактически вычисленное значение может не сколько превышать единицу, что соотвотствует положению точки х после конца ребра р и такая точка может оказаться необнаруженной.
С целью обойти подобное затруднение при вычислении точки пересеченш двух ребер в программе convexPolygonlntersect применяется функцш crossingPoint. Для заданных двух ребер e и f функция сначала вычисляет точку, в которой пересекаются бесконечные прямые линии, определяемые ребрами e и f. Если эта точка оказывается в непосредственной близости одного из четырех концов упомянутых ребер, то в качестве точки пересе чения берется ближайшая концевая точка. В силу особенностей применении функция работает с параметрическими значениями, а не с самими точками. Путем расширения диапазона параметрических значений вдоль ребра f ребро фактически удлиняется на величину EPSILON2 в обоих направлениях. Если точка пересечения при вычислении находится в пределах EPSILON2 от одной из концевых точек ребра f, то точка пересечения принудительно "привязывается" к этой концевой точке. То же самое правило применяет и к ребру е.
Функция crossingPoint возвращает одно из значений COLLINEAR, PARALLEL, SKEW_NO_CROSS или SKEW_CROSS (коллинеарны, параллельны, не пересекаются, пересекаются), показывающее взаимное положение ребер е и f. Если возвращается значение SKEW_CROSS, показывающее, что ребра имеют точку пересечения, то эта точка пересечения возвращается через ссылочный параметр р:
#define EPSILON2 1E-10
int crossingPoint(Edge &e, Edge &f, Point &p)
{
double a, t;
int classe = e.intersect(f, s);
if ((classe == COLLINEAR) || (classe == PARALLEL))
return classe;
double lene = (e.dest-e.org).length();
if ((s < -EPSILON2*lene) (((s > 1.0+EPSILON2*lene))
return SKEW_NO_CROSS;
f.intersect(e, t);
double lenf = (f.org-f.dest).length();
if ((-EPSILON2+lenf <= t) && (t <= 1.0+EPSILON2*lenf)) {
if (t <= EPSILON2*lenf) p = f.org;
else if (t >= 1.0-EPSZLON2*lenf) p = f.dest;
else if (s <= EPSILON2*lene) p = e.org;
else if (a >= 1.0-EPSILON2*lene) p = e.dest;
else p = f.point(t);
return SKEW_CROSS;
} else
return SKEW_NO_CROSS;
}
Если в качестве основы для вычисления точек пересечения брать функцию crossingPoint, то наша программа определения пересечения выпуклых полигонов будет устойчиво работать даже тогда, когда полигоны пересекаются в вершинах. Но заметим, что наша программа может дать ошибку, если вершины одного из полигонов располагаются очень близко (в пределах EPSILON2) от границ другого полигона, но практически не касаясь границы.
|