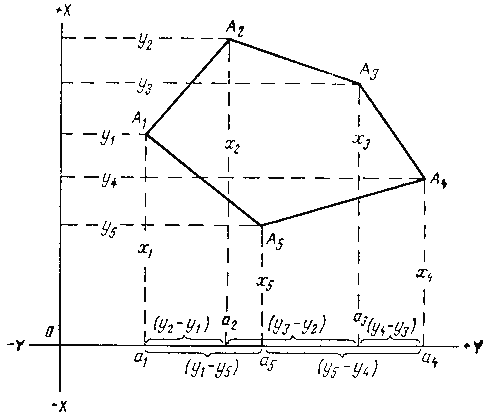
Пусть требуется определить площадь полигона A1, A2, A3, A4, A5 с координатами вершин x1,y1; x2,y2; x3,y3; x4,y4; x5,y5. Площадь полигона S можно представить трапециями, у которых абсциссы являются основаниями, а разности ординат соседних точек высотами
S = a1A1A2a2 + a2A2A3a3 + a3A3A4a4 - a5A5A4a4 - a1A1A5a5.
2S = (x1 + x2)(y2 - y1) + (x2 + x3)(y3 - y2) + (x3 + x4)(y4 - y3) + (x4 + x5)(y5 - y4) + (x5 + x1)(y1 - y5). (1)
После раскрытия скобок и приведения подобных членов получим
2S = x1y2 - x2y1 + x2y3- x3y2 + x3y4 - x4y3 + x4y5 - x5y4 + x5y1 - x1y5 (2)
После вынесения за скобки x1, x2, x3, x4, x5 будем иметь
2S = x1(y2-y5) + x2(y3-y1) + x3(y4-y2) + x4(y5-y3) + x5(y1-y4)
а если из формулы (2) вынести за скобки y1, y2, y3, y4, y5. то будем иметь
2S = y1(x5-x2) + y2(x1-x3) + y3(x2-x4) + y4(x3-x5) + y5(x4-x1).
В сокращенном виде эти формулы можно записать так:
После преобразований получаем формулу в ее нормальном виде.
Аналогичное можно проделать и для любого другого многоугольника.
|