Up to now, we have met all fundamental parts of Fortune's method and so we can think about an
implementation. However, let us say just a word about termination condition. When all points
are behind the scanning line and all events have been handled, Voronoi diagram is not fully
constructed yet. We have to construct the remaining half-lines. For this purpose, the whole
diagram is surrounded by a box (Figure 6) on which border all half-edges terminate.
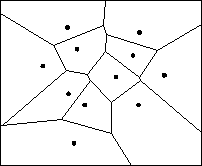
Figure 6: Completely defined computer represented Voronoi diagram does not contain any half-edges
The following algorithm summaries the consideration done up to now and shows the core of the
Fortune's method.
VORONOI_DIAGRAM(P)
Input: A set P of point sites in the plane
Output: The Voronoi diagram Vor(P) given inside a bounding box
in a doubly-connected edge list structure
{
Initialize the event tree Q with all point events
while Q is not empty do
{
Consider the event with largest y-coordinate in Q
if the event is a point event, occurring at site pi
then HANDLE_POINT_EVENT(pi)
else HANDLE_CIRCLE_EVENT(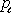 )
Remove the event from Q
}
Put Voronoi diagram into a box
} )
Remove the event from Q
}
Put Voronoi diagram into a box
}
|