The binary tree as a data structure for keeping the parabolic front is not chosen just because
of quick updating, but also because the topological structure of the parabolic front can be
represented the most naturally by the binary tree (Figure 8).
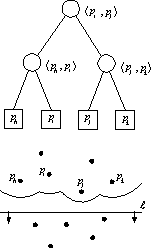
Figure 8: The representation of a topological structure of the parabolic front
The arcs on the parabolic front are represented by the tree leaves while joints between arcs
are stored by the interior tree nodes. The most left arc on the parabolic front is represented
by the most left leaf in the tree, the second left most arc is represented by the next left most
leaf and so on.
Of course, the most interesting operation is inserting and deleting the parabolic arcs from the
data structure. As we mentioned in section 2.1, when a point event happens, a new arc appears
also on the parabolic front by dividing the existed arc upon the event point. In the data
structure representing the parabolic front, this is manifested as replacing the leaf with a
sub-tree. As shown in Figure 9, the sub-tree consists of three nodes; the middle one represents
the new arc and the other two the divided parts of the old arc.
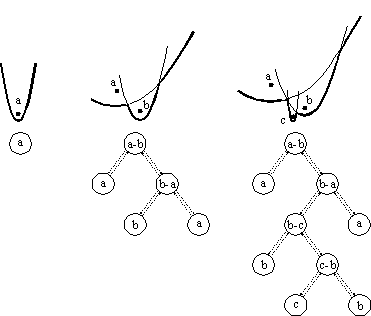
Figure 9: Inserting a new arc into the tree representing the parabolic front
As we said in section 2.2, an arc shrinks to a point and disappears from the parabolic front at
the circle event. In the tree representing the parabolic front, this reflects as deleting a
leaf from the tree. However, with the leaf we must delete also the upper internal node and the
second internal node becomes new joint point of two neighboring arcs. The circle event determines
which arc has to be deleted. Both neighbors can be found as left and right leaf of disappearing
leaf. The first node is trivial to find, because it is the father of the disappearing leaf. But
finding the second node is not easy. We have to know on which side of the point, defining the
disappearing arc the second node is. The second node is determined as an intersection node of
two searching directions (see Figure 10). The first starts from the disappearing arc and the
second from the left (if we divide arc on the left side) or the right neighbor (if the arc on
the right side is being divided). The intersection node represents joint of two neighboring arcs.
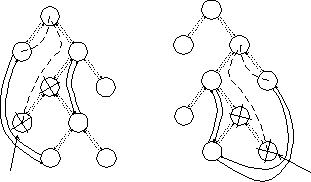
Figure 10: Two possibilities of deleting an arc from the tree of the parabolic front
To complete the explanation of this structure, a few words is needed to explain the attributes
stored in the nodes and the leaves. We are interested especially in pointers between the tree
of the parabolic front and other structures. We are also interested in how the parabola is
stored in the tree. Let us remember that there is no need to store a real parabola; it is enough
to store just a point, which defines the parabola. This can be seen from the following equation [BERG97]:
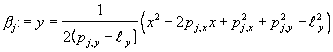
where 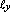 represents the scanning line at the moment of
observation and represents the scanning line at the moment of
observation and  represents the point from P,
which defines the arc represents the point from P,
which defines the arc 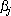 . .
Internal nodes of the tree the pointers pointing to the edge in the data structure of Voronoi
diagram are stored. In this way, each edge belonging to the Voronoi point is directly accessible,
when the circle event is serviced and so there is no need to perform any search operations in the
data structure of Voronoi diagram. At the leaves of the tree, a pointer to the circle
event is stored, if the arc defines a circle event. If not, pointer is set to NULL. By maintaining
this pointer, we do not have to perform any search after encountering false events.
|