Алгоритм CHM.

 

В 1989г Cheriyan, Hagerup & Mehlhorn предложили очень интересную модификацию алгоритма Голдберга-Таряна. В оригинальном алгоритме поток из одной вершины в другую перемещается по текущей допустимой дуге. После того, как текущая дуга станет недопустимой, необходимо выбрать следующую текущую дугу. Четкого правила выбора следующей текущей дуги не давалось.

В предлагаемом алгоритме рассматривается неориентированная сеть. Максимальный поток вычисляется в фазах с помощью “неполного” графа {V, E’}, где E’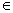E. Дуги в этот вспомогательный граф добавляются по очереди, в порядке, позволяющем дуге стать насыщенной после добавления. Вместо функции избытка e(v), используется функция “явного” избытка e’(v) = max{e(v) - ∑ c(v, u), 0}. Функция явного избытка используется, что бы определить максимальную величину потока, который может быть “вытолкнут” из вершины v.

Так же как и в алгоритме Голдберга-Таряна, здесь используются динамические деревья, позволяющие быстро изменять поток в цепи. Все дуги в лесу должны быть допустимыми для операции Push. Каждый узел может иметь максимум одну исходящую дугу. Во время насыщения дуги, она удаляется с помощью операции Cut. Во время выполнения операции Relabel(v), все направленные в v дуги удаляются из дерева. При выборе для вершины новой допустимой текущей дуги, она добавляется в дерево с помощью Link.

Алгоритм не имеет ограничения k на размер структуры. Операция TreePush_Relabel может применяться не только к корню дерева.

Cheriyan, Hagerup & Mehlhorn удалось доказать, что в случае выбора допустимой дуги случайным образом, оценка быстродействия алгоритма с высокой степенью вероятности будет равна O(mn + (nLogn)²). Самым интересным является метод, с помощью которого была доказана подобная оценка.

Рассмотрим игру, игроками в которой являются алгоритм (игрок) и его “соперник”. Пусть дана сеть G = (V,E). Построим для нее “игровое поле” – двудольный граф G’ = (U’, V’, E’), такой, что для каждой вершины w из V и для всех k от 1 до 2n-1, в этом графе вершины u_w,k 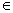 U’ и v_w,k-1  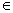V’. Общее число вершин O(n²). Для всех дуг (w, w’) из E, существуют 2n-1 их копии: (u_w,k, v_w’,k-1) для k = 1, …, 2n-1.

Назначение ребра из каждого u_w,k означает выбор алгоритмом текущей дуги для вершины w, при d(w) = k.

Поведение соперников связано с вычислением максимального потока следующим образом:

Когда вершине w присваивается метка k, все игровые дуги, инцидентные u_w,k, кроме той, что является текущей допустимой, удаляются из G’.

Когда метка w меняется с k на k+1 (в процедуре Relabel), мы должны удалить (процедурой cut) все входящие в w дуги из леса F. В игре, соперник игрока удаляет вершину v_w,k, и получает очко за каждое назначенное ребро инцидентное v_w,k. (ребра также удаляются). Т.е. каждое удаление ребра из F соответствует очку, получаемому соперником.

Когда дуга насыщается, соответствующая ему дуга в G’ (с необходимыми значениями k) удаляется соперником. Т.е. удаление соперником дуги (ход edge-kill) соответствует приведшей к насыщению операции Push.

Когда игрок (алгоритм) выполняет переназначение дуги, в алгоритме поиска максимального потока происходит смена текущей дуги. Старая текущая дуга должна быть удалена из F, что опять же приносит очко сопернику.

Пусть число очков, набранных соперником, равно P(n, m), тогда P(n², mn) – верхняя оценка числа дуг, которые были удалены из F до того, как были насыщены. Число edge-kill ходов соперник является числом операций Push, приведших к насыщению дуги.

Cheriyan, Hagerup и Mehlhorn доказали, что оценка подобного алгоритма равна O(mn + n^3/2m^1/2 + P(n², nm)Logn + C(n², mn)), где P(n.m) – максимальное число очков, которое смог собрать соперник, а C(n, m) – стоимость реализации стратегии алгоритма-игрока. Они рассмотрели случайную стратегию выбора текущей дуги. Реализуется она таким образом: всем инцидентным дугам ставится в соответствие случайное число, затем выбирается допустимая дуга с минимальным номером. Алгоритм с подобной стратегией они оценили O(mn + (nLogn)²). [1]