Алгоритм Голдберга-Рао.

 

Этот, достаточно современный (1997г) алгоритм, впервые превзошел считавшуюся непреодолимой оценку O(nm). Его результат: O(min{n^2/3,n1^/2}m Log(n²/m)LogU). Алгоритм является слабо-полиномиальным, но, учитывая теорему подобия Габова (Gabow), в которой для сравнения слабо- и сильно-полиномиальных алгоритмов используется LogU = O(Log n), он является лучшим на данный момент.

В каждой своей итерации, алгоритм Голдберга-Рао ищет тупиковый поток, используя неединичную функцию для определения длины допустимых дуг. Идея использования неединичной функции уже рассматривалась многими учеными[1], но никогда не давала улучшения асимптотической оценки быстродействия.

Введем основные определения. Пусть G = (V, E) – ориентированная сеть с источником s и стоком t. Функция c(e): E 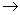 {1, …, C} определяет пропускные способности дуг. Потоком, соответственно назовем функцию f(e): E 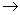 {1, …, C}, для которой выполняются f(e)  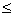c(e) и принцип сохранения потока. Остаточной пропускной способностью является c_f(i, j) = f(I, j) + c(i, j) – с(i, j). Дуги, имеющие положительную c_f, составляют множество E_f. Граф G_f = (V, E_f) является сетью остаточных пропускных способностей. Остаточный поток – это разница между некоторым оптимальным потоком в сети (f^*) и текущим. f^R: |f*(e) – f(e)|. Под тупиковым потоком будем понимать функцию, при которой в графе G_f не существует пути из s в t.

Функцией длины дуги является функция l: E 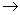 R⁺. Назовем функцию d: V 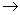 R⁺ меткой дистанции относительно l, если d(t) = 0 и для всех дуг e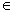E, остаточная стоимость не отрицательна. Остаточная стоимость определяется как l_d(i, j) = l(i, j) + d(j) – d(i). Остаточная стоимость на дугах пути из s в t может только возрастать. Обозначим d_l(i) дистанцию вершины i до t относительно l. Заметим, что .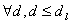

С помощью функции длины дуги можно получить верхнюю границу остаточного потока. Дугу из E_f можно рассматривать как канал шириной c(e), длиной l(e) и площадью vol(e) = c(e)l(e). Площадью сети (Vol_fl) будет сумма площадей всех дуг с положительной остаточной пропускной способностью. Т.к. каждая единица остаточного потока требует d(s) единиц площади, то верхней оценкой величины остаточного потока будет Vol_fl/d(s). Назовем дугу (i, j) из E_f допустимой, если d(i) > d(j), или d(i) = d(j), если l(i, j) = 0. Подобные дуги формируют множество A(f, d, l) и составляют граф G_A = (V, A(f, d, l)).

Алгоритм Голдберга-Рао базируется на бинарной функции длины дуги. Она равна нулю на дугах с “большой” остаточной пропускной способностью и единице на остальных. Это позволяет уменьшить Vol_fl и получить лучшею оценку для остаточного потока по сравнению с единичной функцией длины дуги. Определение “больших” и “маленьких” остаточных пропускных способностей зависит от текущей величины остаточного потока. Обозначим F верхнюю оценку остаточного потока. Изначально она равна 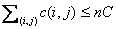 и корректируется по ходу выполнения алгоритма. Если пропускные способности и величина потока являются целыми числами, алгоритм должен прекратить свою работу, как только F станет меньше единицы. Под фазой работы алгоритма будем понимать вычисления, которые были произведены между двумя изменениями значения F. Каждая фаза состоит из шагов.

Текущее значение F определяет величину. - это величина, на которую мы пытаемся увеличить поток на каждом шаге данной фазы. Бинарная функция длины l(e) равна 0, если c_f(e)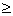3 и 1 в противном случае. Длина некоторых дуг должна изменятся после наращивания потока в сети с помощью тупикового потока. Назовем дугу (i, j) особой, если 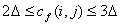, d(i) = d(j) и 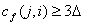. Определим функцию l^’, равную 0 на всех особых дугах и совпадающую с l на остальных. Заметим, что d_l = d_l’.

В начале каждого шага, мы вычисляем d_l, j’ и d_l’. Заметим, что G_A может иметь циклы из дуг нулевой длины. В этом случае следует удалить из графа компоненты сильной связности, порожденные дугами нулевой длины, и увеличивать поток в полученном графе.

На каждом шаге в полученном ациклическом графе либо находится тупиковый поток, либо поток величины .

Изменение F можно выполнить несколькими способами. Напр., если Vol_fs/d_l(s) 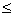 F/2, то завершим фазу и положим F = Vol_fs/d_l(s). Другим способом является определение F через разрез сети. Назовем текущим разрезом, разрез (S, T), для которого выполняется c_f(S, T) 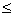 F. В этом случае завершать фазу следует, как только найден разрез (S’, T’) 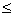 F/2 и положить (S, T) = (S’, T’), а F = c_f(S’, T’). Реализация алгоритма, основанная на использовании разрезов, имеет множество плюсов. Подробно она описана в [11].

В общем виде работу алгоритма на i-той фазе можно представить так:

Имеются значения l и d_l. До тех пор, пока F не уменьшилось, выполняем следующее:

1.      Вычислить Vol_fs. Если Vol_fs/d_l(s) 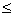 F/2, изменить F и завершить фазу.

2.      Вычислить l’.

3.      Получить ациклический граф.[2]

4.      Найти в полученном графе тупиковый поток, либо поток величины .

5.      Увеличить поток в исходной сети с помощью найденного.

6.      Вычислить l и d_l.

 

Для нахождения тупикового потока можно воспользоваться любым подходящим алгоритмом. Если величина найденного потока X >, то избыток следует устранить. Установим величину избытка в стоке, равную X- (это искусственная операция, избытка в стоке не может быть по определению)  Затем, необходимо рассмотреть вершины в обратном порядке, начиная со стока. В каждой вершине нужно уменьшать величину потока на входящих в нее дугах, до тех пор, пока избыток в ней не исчезнет.