Алгоритм Голдберга-Таряна (Goldberg-Tarjan).
Опубликован в 1986г. Алгоритм
основан на идее предпотоков Карзанова, но не использует поиск тупикового потока
в фазах. Оценка быстродействия алгоритма: O(n3),
но может быть улучшена до O(nmLog(n2/m)), если алгоритм реализован с
использованием динамических деревьев Слейтора. Также имеется версия алгоритма
для параллельных вычислений с оценкой O(n2Logn) на n процессорах. В основе алгоритма лежат
2 операции: наращивание потока (Push)
и изменение метки вершины (Relabel),
в связи с этим, метод примененный в алгоритме получил название Push-Relabel. Данный метод внес большой вклад
в исследование проблемы максимального потока. Многие современные алгоритмы
основаны на Push-Relabel методе.
Рассмотрим неориентированную
сеть G. Дадим следующие
определения:
Функция избытка: e(v) = - div (v) = ∑ f(v’,v) - ∑ f(v,v’’).
Псевдопотоком назовем функцию f, удовлетворяющую
ограничениям пропускных способностей дуг и антисимметричности.
Антисимметричность означает что f(v, w) = - f(w, v).
Понятие антисимметричности предложено Слейтором и служит двум целям. Во-первых,
оно исключает возможность существование положительного потока как в направлении
(u, v), так и в направлении (v, u). Во вторых, оно упрощает некоторые
определения, например, закон сохранения потока.
Предпотоком является
псевдопоток на пути из s
в t, для всех вершин
которого e(v) ≥ 0 (кроме s).
Под rf(v,w) будем понимать остаточную пропускную способность дуги (v, w). Gf – сеть остаточных пропускных способностей потока f.
Каждой вершине сети сопоставим
метку d(v) ≥ 0, обладающую
следующими свойствами: d(t) = 0, d(s) = n,
для 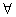 r(v, w)
r(v, w) 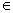 Gf d(v) ≤ d(w) + 1. Если d(v) < n, то под ней можно понимать дистанцию
до стока в Gf,
иначе d(v) – n – дистанция до источника Gf.
Gf d(v) ≤ d(w) + 1. Если d(v) < n, то под ней можно понимать дистанцию
до стока в Gf,
иначе d(v) – n – дистанция до источника Gf.
Назовем вершину активной, если
она не является источником или стоком и имеет положительный избыток (e(v) > 0).
Рассмотрим базовые операции:
Push(v, w).
Увеличивает поток из v
в w на q, где q = min{e(v), r(v, w)}.
Очевидно, что вершина v
должна быть активной, дуга (v,
w) не насыщенной, а d(v) = d(w) + 1.
Relabel(v). Обновление метки вершины v. Вершина должна быть
активной, и для 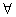 w с r(v, w) > 0 должно выполнятся d(v)
≤ d(w). Relabel устанавливает d(v) = min(d(w)+1|
w с r(v, w) > 0 должно выполнятся d(v)
≤ d(w). Relabel устанавливает d(v) = min(d(w)+1| 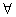 (v,w)
(v,w) 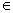 Ef), где Ef – множество дуг
сети остаточных пропускных способностей относительно потока f.
Ef), где Ef – множество дуг
сети остаточных пропускных способностей относительно потока f.
Push_Relabel(v).
Пока e(v) не станет нулевой или не изменится d(v) выполняем внутренний цикл:
Пусть (v, w) – текущая дуга в списке a(v).
Рассмотрим 2 случая.
a). Операция Push применима к (v, w). В этом случае производим увеличение потока и, если вершина w стала активной, помещаем ее
в конец очереди X.
б). Push не применима к (v, w). Тогда, если (v,
w) не последняя дуга в a(v), то делаем текущей следующую дугу
списка. Если же (v, w) последняя дуга, то
выполняем Relabel(v) и выбираем текущей первую
дугу в a(v). В [10]
доказана применимость Relabel
к v после обработки
всех дуг a(v).
Общая логика работы алгоритма
такова:
Инициализация.
В смежные источнику вершины v посылается поток величины c(s, v). Поток на остальных дугах нулевой. Смежные с источником
вершины становятся избыточными, избыток в остальных вершинах отсутствует.
Расставим метки: d(s) = n, для всех остальных вершин d(v) = 0.
Поместим все активные вершины в очередь X. Также нам потребуются
списки всех исходящих дуг a(v) для каждой вершины. В этих
списках будет выбрана “текущая дуга” (при инициализации текущей дугой
выбирается первая дуга в списке).
Главный цикл.
До тех пор, пока очередь X не пуста, извлекаем вершину
v из очереди и
выполняем Push_Relabel. Проверим, не
перестала ли вершина v
быть активной. Если нет – добавляем ее в конец X. Переходим к следующей вершине очереди
X.
Применение динамических
деревьев в алгоритме Голдберга-Таряна.
Без использования деревьев
Слейтора-Таряна алгоритм имеет оценку быстродействия O(n3), что повторяет достижение Карзанова. Рассмотрим
набор корневых, не имеющих общих вершин деревьев. Каждой вершине сопоставим
число g(v), которое может
дополнительно принимать значение + ∞ и - ∞. g(v) – это пропускная способность исходящей из v дуги. Пусть p(v) – множество предков вершины v, P(v) – смежный с v предок. Примем условие, что
любая вершина v для самой себя одновременно и предок, и
потомок. Введем следующие операции:
Root(v) – аналогична операции в деревьях Слейтора-Таряна.
Size(v) – возвращает число вершин в дереве, которому принадлежит v.
Value(v) – аналог процедуры Cost для дуг. Возвращает g(v).
Find_min(v) –
возвращает ближайшего к корню предка w 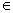 p(v), с минимальным g(w).
p(v), с минимальным g(w).
Update(v, x) – добавляет x
к g(w), для каждого w 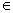 p(v). (- ∞ + ∞ = 0).
p(v). (- ∞ + ∞ = 0).
Link(v, w) –
соединяет деревья, которым принадлежат вершины v и w, делая v
потомком w. Если v и w принадлежат одному дереву или v не является корнем, то
процедура завершается, не изменяя деревьев.
Cut(v) – Делит дерево на два, удаляя дугу из вершины v к ее предку. Если v – корень, то процедура не
применяется.
Динамические деревья
используются для хранения текущих дуг вершин. Во время инициализации все
вершины представляют собой набор корней деревьев без дуг. g(v) всех вершин = ∞. Дуги дерева являются подмножеством
текущих дуг вершин сети. В дерево могут быть добавлены только допустимые
текущие дуги. Назовем текущую дугу (v, w)
вершины v 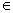 V \ {s, t} допустимой, если d(v) = d(w) + 1 и rf(v, w) > 0. Дуга (v,
w) добавляется в дерево
так, что w = P(v). Ограничим размер дерева числом k, где k = n2/m
(объяснение подобного решения см. в [10]).
V \ {s, t} допустимой, если d(v) = d(w) + 1 и rf(v, w) > 0. Дуга (v,
w) добавляется в дерево
так, что w = P(v). Ограничим размер дерева числом k, где k = n2/m
(объяснение подобного решения см. в [10]).
Опишем следующие процедуры:
1. Clear(v) – удаление всех дуг с нулевой пропускной способностью.
Пока Value(Find_min(v)) = 0 выполнять: u := Find_min(v); Cut(u); Update (u, +
∞).
2. Send(v) - “проталкивает” избыток вершины v в корень дерева:
До тех пор, пока вершина v не стала корнем дерева, или
избыток вершины не стал равен 0, выполняем Update(v,
-q),где q = min{e(v), Value( Find_min(v) )}
и Clear(v). Процедура Send применима только к
активным вершинам.
3. TreePush_Relabel(v) - применима только если v активна и является корнем
дерева. Рассмотрим текущую дугу (v, w)
вершины v. Имеются 4
случая:
а.) Дуга допустима и Size(v) + Size(w)
≤ k. Тогда делаем
v потомком w, выполняя Update(v, - ∞) (чтобы получить g(v) = 0), Update(v, rf(v,
w)) и Link(v, w). И
“проталкиваем” поток: send(v)
б). Дуга допустима и Size(v) + Size(w)
> k. Выполняем Send(w).
в). Дуга не допустима и не
является последней в списке a(v). Выбираем следующую
текущую дугу из списка.
г). Дуга не допустима и
последняя в a(v). Выбираем текущей дугой
первую дугу списка. Выполняем Cut(v, w). Для всех потомков u вершины v выполняем Update(u, ∞). В завершение, вызываем Relabel(v).
Заменив в главном цикле
процедуру Push_Relabel на TreePush_Relabel, мы получим алгоритм поиска
максимального потока для динамического дерева.
В своей статье Голдберг и Тарян
предложили также ряд эвристик, которые не влияют на асимптотическую оценку
алгоритма, но могут увеличить его быстродействие на практике. Например
периодическое обновление меток вершин в сети остаточных пропускных
способностей, с помощью поиска в ширину из источника в сток и из стока в
источник. Такой поиск позволит получить для вершины v расстояние до стока d(v, t) и
до источника d(v, s). В качестве d(v) следует выбрать min{d(v, s) + n, d(v, t)}. Есть несколько вариантов выбора
момента проведения этого уточнения. Например, через каждые k операций Relabel, или каждый раз, когда
насыщается дуга, ведущая в сток, либо поток по исходящей из источника дуге
окажется нулевым.
Благодаря “гибкости” своей
реализации, возможности распараллеливания вычислений и высокому быстродействию
на большинстве типов сетей, Push-Relabel методы получили
широкое распространение на практике.