Алгоритм Малхотри-Кумара-Махешвари.

 

В 1978г Малхотри, Кумару м Махешвари (Malhotra, Pramodh Kumar, and Maheshwari) удалось с помощью модификации алгоритма Диница получить алгоритм с оценкой O(n³) и тем самым повторить результат Карзанова.

“Потенциалом” вершины сети (далее P(v)) назовем максимальное количество потока, которое может быть пропущено через вершину. Очевидно, что потенциал является минимумом из суммарной пропускной способности входящих в вершину дуг (Pi(v)) и суммарной пропускной способности исходящих дуг (Po(v)). Для источника и стока потенциал равен Pi(v) и Po(v) соответственно.

Изменим процедуру нахождения псевдомаксимального потока в Sk сети.

Для каждой вершины сети вычислим ее потенциал. До тех пор, пока Sk содержит вершины с ненулевым потенциалом, выполнятся следующее:

1.      Поместим все вершины с нулевым потенциалом в стек. Пока стек не окажется пуст, извлекаем вершины из стека и удаляем их вместе с инцидентными им ребрами, уменьшая потенциалы смежных вершин. Если потенциал смежной вершины окажется равным 0, то она также помещается в стек.

2.      Найдем вершину v с минимальным потенциалом p = P(v).

3.      Построим поток из v в сток t величины p. Для этого увеличиваем поток на исходящих из v дугах, до тех пор, пока его величина не достигла p. Используются только согласованные допустимые дуги. Теперь в вершинах v’ инцидентных дугам, по которым пустили поток, находится некоторая величина p’i. Величина p’i гарантированно может быть “продвинута” дальше, т.к. p’i ≤ p, а для 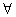v, p ≤ Pi(v).  Для каждой такой вершины повторяем процедуру увеличения потока, пока величина достигшего стока потока не будет равна p. На практике эту процедуру удобно реализовать с помощью поиска в ширину.

4.      Построим поток из v в источник s величины p аналогично предыдущему пункту.

5.      Из 3 и 4 следует, что построенный в Sk поток является потоком из s в t. Перенесем его в исходную сеть, либо “запомним” в какой либо структуре. Скорректируем сеть аналогично процедуре из алгоритма Диница, изменяя потенциалы инцидентных удаляемым дугам вершин.

Поток, образованный объединением полученных на каждой итерации потоков, является псевдомаксимальным для S_k.