Динамические деревья Слейтора-Тарьяна.
Слейтор
и Тарян в 1981г. разработали на основе деревьев,
использованных в алгоритме Галила-Наамада, улучшенную
структуру данных. Их динамические деревья позволяют производить операции
слияния (link) и
разделения (cut) за
время O(log n). Модификации деревьев Слейтора-Таряна используются для повышения оценки
быстродействия практически во всех современных алгоритмах.
Для хранения информации о
различных путях в сети и быстрого изменения этой информации, предлагается
воспользоваться лесом деревьев. Одна и та же вершина сети не может одновременно
содержаться в двух деревьях. Деревья допускают над собой два вида операций –
слияния (link) и
разделения (cut).
Link(v, w) – соединяет две вершины из различных деревьев, добавляя дугу (v, w). В результате 2 дерева сливаются в
одно.
Cut(v, w) – Разделяет дерево, содержащее дугу (v, w) на два, с помощью удаления дуги (v, w). Вершины v
и w должны быть
смежными вершинами одного дерева.
Следует различать корневые и
свободные деревья. В случае корневых деревьев операция Link(v, w)
разрешена, только если v
– корень дерева. Результатом слияния будет дерево с корнем, равным корню
дерева, которому принадлежала вершина w. Предполагается, что дуги корневого дерева ориентированы по
направлению к корню, т.е. от потомка к родительскому узлу. Заявленная оценка
быстродействия справедлива как для корневых, так и для свободных деревьев.
Для применения подобной
структуры к сетевым задачам, вводятся также 5 дополнительных операций:
Root(v) – возвращает корень дерева,
содержащего v.
Cost(v, w) – возвращает “стоимость” (вес) дуги (v, w), т.е. вещественной число.
Find_min(v) – возвращает дугу минимальной
стоимости на пути из v
к корню дерева, в котором находится v. Если этот путь не содержит дуг, возвращается специальное null значение. Если дуг
минимальной стоимости несколько, результатом будет ближайшая к корню дуга.
Update(v, x) – увеличивает стоимость всех дуг пути из v к корню дерева, в котором находится v, на x. x – вещественное число.
Evert(v) - изменяет дерево, содержащее вершину v, делая v корнем этого дерева.
Операция Link модифицируется для трех параметров:
Link(v, w, x) – отличие лишь в том, что добавляемой дуге (v, w) присваивается стоимость x.
Первых 6 операций достаточно
для применения деревьев Слейтора-Таряна к задаче о
поиске тупикового потока. Операция Evert необходима лишь в случае
использования свободных деревьев.
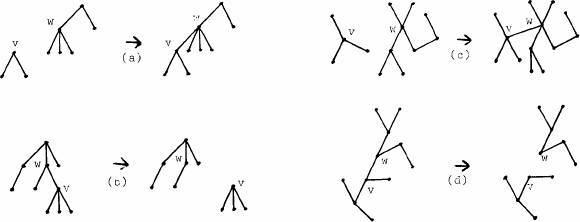
рис. 10.
а). Операция Link в корневом дереве. b). Операция Cut в корневом дереве.
c). Операция Link в свободном дереве. d). Операция Cut в свободном дереве
Иллюстрации из [9].
Нахождение тупикового потока с
помощью динамических деревьев.
Инициализация. Помещаем в нашу структуру все вершины сети (без
дуг), получим множество “деревьев”, состоящих из одной изолированной вершины.
Шаг 1. Пусть v
= root (s). Если v = t, перейдем к шагу 4 иначе к шагу 2.
Шаг 2. (v
≠ t). Если из
вершины v не исходит ни
одной дуги, перейдем к шагу 3. Иначе, выбираем дугу (v, w), выполняем Link(v, w, c(v, w)) и переходим к шагу 1.
Шаг 3. (все пути из v
в t блокированы). Если v = s, прерываем работу алгоритма. Иначе,
для всех входящих в v
дуг (содержащихся в этом дереве) выполняем cut(u, v), и переходим к Шагу 1.
Шаг 4. (s и
t в одном дереве, t = root(s), путь из s
в t – увеличивающий
поток путь). Пусть (v, w) = Find_min(s). (нашли дугу минимальной
пропускной способности). Пусть cmin = cost(v, w). Выполняем Update(s, -cmin) и
переходим к шагу 5.
Шаг 5. (удаление дуг с нулевой пропускной способностью). Пусть (v, w) = Find_min(s).
Если cost(v, w) = 0, то cut(c, w) и
выполняем шаг 5 заново. Иначе переходим к шагу 1.
После окончания работы цикла,
максимальный поток определяется разницей пропускных способностей дуг до и после выполнения алгоритма. Результат будет получен за O(nmLogn).
Деревья Слейтора-Таряна
(и их модификации) применяются не только для нахождения тупиковых потоков, они
используются в задаче нахождения наиболее удаленного от корня общего предка для
двух заданных вершин, задаче нахождения поддеревьев минимальной стоимости при
различных условиях (для решения используются свободные деревья) и в симплекс
методе решения сетевых задач.