
|
Решение задачи 1.
Даны 2 точки A(x1,y1) и B(x2,y2). Определить, какой из отрезков, OA или OB, образует больший угол с осью OX.
В курсе высшей алгебры показывается, что если
D=x1*y2-x2*y1<0,
то угол, определяемый точкой A больше, чем угол, определяемый точкой B; если D=0, то углы равны, и если D>0, то угол, образуемый OB, больше.
Например:
A(-1,3), B(0,-2), x1*y2-x2*y1=2>0,
и следовательно, отрезок OA образует меньший угол с осью OX (угол всегда отсчитываются против часовой стрелки !).
[Назад]
Решение задачи 2.
Как определить, принадлежит ли точка A(x,y) отрезку с концевыми точками B(x1,y1) и C(x2,y2)?
Точки отрезка z можно описать уравнением
pOB+(1-p)OC=z, 0<=p<=1, OB и OC - векторы.
Если существует такое p, 0<=p<=1, что
pOB+(1-p)OC=A,
то A лежит на отрезке, иначе - нет.
Равенство (*) расписывается по координатно так:
px1+(1-p)x2=x
py1+(1-p)y2=y
Из первого уравнения находим p, подставляем во второе: если получаем равенство и
0<=p<=1, то A на отрезке, иначе - нет.
[Назад]
Решение задачи 3.
Найдем какую-нибудь внутреннюю точку A(x,y) выпуклого многоугольника, например, центр масс трех последовательных точек на контуре: A(x,y)=((x1+x2+x3)/3;(y1+y2+y3)/3).
На контуре выберем произвольно две последовательные вершины L1 и L2 и вычислим углы, которые образуют отрезки (A,L1) и (A,L2) с осью OX. Если первый угол меньше второго, то обход против часовой стрелки, иначе - по часовой. Для вычисления углов можно использовать функцию arctan(x) в Pascal.
Рассмотрим чуть другую задачу:
Даны 2 точки A(x1,y1) и B(x2,y2). Определить, какой из отрезков,OA или OB, образует больший угол с осью OX. (Предыдущая задача очевидным образом сводится к этой задаче 1).
Если в условии задачи многоугольник невыпуклый, то можно предложить следующий способ решения: находим точку с максимальной абсциссой, и, идя вдоль контура, смотрим: если первое невертикальное ребро отклоняется против часовой стрелки, то это обход против часовой стрелки, иначе - нет.
[Назад]
Решение задачи 4.
Пусть a,b и c - длины отрезков XY, YZ и ZX соответственно. Если перпендикуляр P попадает на отрезок XY, то углы XYZ и YXZ по величине не превосходят 90 градусов (эти оба угла не тупые).
По теореме косинусов
B2 = A2 + C2 - 2*A*C*cos YXZ
и
C2 = A2 + B2 - 2*A*B*cos XYZ
Если углы XYZ и YXZ не тупые, то cos YXZ и cos XYZ лежат в пределах от 0 до 1, и слaгаемые -2*B*C*cos YXZ и -2*A*B*cos XYZ в приведенных выше формулах неположительны, т.е. в случае, когда перпендикуляр попадает на отрезок XY, должны выполняться одновременно два неравенства
B2 <= A2 + C2
и
C2 <= A2 + B2,
Если хотя бы одно неравенство нарушается, то перпендикуляр попадает на продолжение отрезка . Примечание :
Квадрат длины отрезка, например, XY, можно найти по формуле
A = (x1-y1)2 + (x2-y2)2
[Назад]
Решение задачи 5
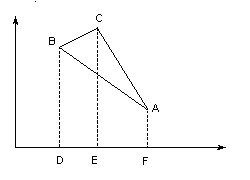 Без нарушения общности считаем, что фигура располагается полностью в одной из полуплоскостей (если это не так, то просто сделаем параллельный перенос). Без нарушения общности считаем, что фигура располагается полностью в одной из полуплоскостей (если это не так, то просто сделаем параллельный перенос).
Площадь фигуры будем вычислять как сумму площадей трапеций
(считаем, что площадь может быть и отрицательной) по формуле
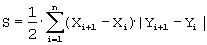
Тут считается, что (XN+1 ,YN+1)=(X1 ,Y1).
Например, для фигуры на рисунке площадь будет вычисляться следующим образом :
SABC = SDBCE + SECAF + SABCF = SDBCE + SECAF - |SABDF|.
Периметр фигуры находится как сумма длин сторон многоугольни-
ка, длина стороны между точками A(x1,y1) и B(x2,y2) вычисляется по хорошо известной формуле
d(A,B)=SQRT((x1-x2)2+(y1-y2)2).
Нахождение угла между сторонами можно свести к задаче нахождения угла между отрезками OD и OP (O - начало координат). Находим (используя функцию arctan в Паскале) угол, образуемый отрезком OP с осью OX, и угол, образуемый OD с OX (при этом необходимо правильно определить значение величины угла - арктангенсы углов 45 и 225 градусов одни и те же; для нахождения истинных величин углов надо еще смотреть, в каких квадрантах расположены точки P и D).
[Назад]
Решение задачи 6.
Вариант 1. Можно через концы отрезка провести прямую cx+d=y и определить, принадлежит ли точка пересечения двух прямых x, если она существует, отрезку. То есть, мы должны решить уравнение x*(c-a)=(b-d), найти y=ax+b, и проверить выполнение неравенств x1<=x<=x2, y1<=y<=y2.
Но при нахождении x при делении могут возникнуть большие вычислительные погрешности или даже переполнение или потеря значимости, в результате чего получится неверный ответ.
Вариант 2. Обозначим F(x,y)=ax+b-y. Прямая ax+b=y разбивает плоскость на три части: в одной F(x,y)>0, в другой F(x,y)<0 и на прямой ax+b=y F(x,y)=0 . Если эта прямая пересекает отрезок, то либо концы отрезка лежат в различных полуплоскостях, либо хотя бы одна концевая точка отрезка лежит на прямой. Это равносильно выполнению следующего неравенства F(x1,y1)*F(x2,y2)<=0. Таким образом, не вычисляя точку пересечения, мы по знаку функционала судим о том, имеют ли прямая и отрезок общую точку. Очевидно, что второй вариант решения подзадачи предпочтительнее первого.
[Назад]
Решение задачи 7.
Выписываем уравнения прямых A и B таких, что концевые точки отрезка 1 принадлежит прямой A, а отрезка 2 - прямой B.
Далее см. решение задачи 6.
[Назад]
Решение задачи 8.
Можно, конечно, из точки Z провести отрезки ко всем 3-м вершинам треугольника, и посмотреть: если сумма площадей трех треугольников ZAB, ZBC, ZCA равна площадей ABC, то точка внутри, иначе - снаружи, но так как все вычисления в машине проводятся с ограниченной точностью, то проверка на равенство ПРАКТИЧЕСКИ НИКОГДА не даст правильного ответа. Вы почти всегда будете получать, что Z вне ABC, не смотря на действительное расположение точки Z. Попробуем решить задачу по-другому:
Принадлежность точки стороне проверяется просто: если концевые точки стороны A(x1,y1) и B(x2,y2), то, если точка Z(x,y) принадлежит стороне, то должно существовать такое число p, 0<=p<=1, что
x=p*x1+(1-p)*x2
y=p*y1+(1-p)*y2
(тут используется то, что если прямая проходит через A и B, то точки прямой имеют координаты (p*x1+(1-p)*x2, p*y1+(1-p)*y2), p действительное число. При 0<=p<=1 мы получаем отрезок между точками A и B).
Далее, проведем из точки Z прямую, параллельную оси OX (ее уравнение будет x=u) и проверим, сколько сторон треугольника пересекает полулуч, идущий от точки Z, например, вправо. Если 0, то Z - вне треугольника, если 1 - то внутри, если 2 - то снаружи (определение пересечения прямой и стороны - задача 6).
Надо конкретно обработать случай, когда прямая пересекает одну из вершин треугольника (например, A).
Может быть 2 случая:
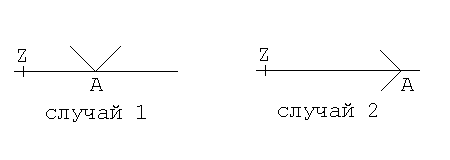
В случае 1, когда оба ребра, входящих в вершину A, лежат по одну сторону от прямой, количество пересечений можно считать равным двум (или нулю), в случае 2, когда ребра лежат по разные стороны от прямой, число пересечений примем равным 1. Проверка, по разные или по одну сторону от прямой лежат концевые точки отрезков - см. задачу 6. Если прямая проходит по стороне, то число пересечений будем считать равным 2.
Аналогично можно проверить, лежит ли точка Z внутри многоугольника (в алгоритме безразлично, выпуклый он или нет). Мы подсчитываем число пересечений луча со сторонами - если оно нечетное, то точка внутри, если четное - то снаружи.
[Назад]
Решение задачи 9.
Один из возможных методов решения. Предположим, мы нашли такую прямую. Будем сдвигать ее в направлении, перпендикулярном этой прямой (параллельный перенос) до тех пор, пока она не пересечет какую-нибудь из концевых точек отрезка. За счет поворота прямой вокруг этой точки мы можем добиться того, что прямая будет проходить через 2 концевые точки отрезков и не перестанет быть решением задачи.
Следовательно, мы должны рассмотреть прямые, проходящие через все возможные комбинации пар концевых точек отрезков. Всего надо проверить (2*N-1)+(2*N-2)+...+1=N*(2*N-1) линий и для каждой из них найти число пересечений с отрезками. Та прямая, у которой это число максимальное, и есть искомая.
При решении возникает подзадача.
Определить, пересекается ли прямая ax+b=y и отрезок с концами (x1,y1), (x2,y2).
Решение ее - см. Задача 6.
[Назад]
Решение задачи 10.
Строим выпуклую оболочку данного множества точек - т.е. такой выпуклый многоугольник, вершинами которого являются некоторые из этих N точек (возможно, не все), что через какое бы ребро этого многоугольника мы ни провели прямую, все N точек исходного множества будут лежать по одну сторону от этой прямой и на ней (определение местоположения точек относительно прямой см. задачу 6).
Из произвольной точки a1 множества A из N точек мы можем провести не более N-1 - го отрезка так, чтобы и вторая концевая точка этого отрезка была из множества A. Берем тот отрезок [a1,a2], для которого все точки множества A лежат по одну сторону от прямой, проходящей через этот отрезок (если любой отрезок не удовлетворяет этому условию, то берем другое a1; с самого начала лучше всего взять в качестве a1 точку с максимальной абсциссой, а если таких несколько, то среди них берем точку с максимальной ординатой -- это гарантирует, что a1 принадлежит искомому контуру выпуклого многоугольника). Для точки a2 ищем точку a3<>a1 так, чтобы все множество A лежало по одну сторону от прямой, определяемой отрезком [a2,a3], ..., для точки ai ищем ai+1<>ai-1 так, чтобы A лежало по одну сторону от [ai,ai+1)], и т.д., до тех пор, пока очередной точкой ai+1 не станет ai - мы замкнули контур, и нашли выпуклую оболочку. Все точки множества A, не лежащие на контуре, лежат внутри выпуклой оболочки.
[Назад]
Решение задачи 11.
Предположим, что мы построили искомый выпуклый многоугольник. Если какая-то точка a (из данного в условии набора S, состоящего из k точек) лежит на стороне многоугольника, то мы считаем ее новой вершиной этого многоугольника. Мы можем считать, что все вершины данного многоугольника есть точки набора S (если это не так, и между двумя точками a и b набора S лежит одна или несколько "посторонних" вершин, то мы можем их отбросить и считать, что a и b - две последовательные вершины контура. Многоугольник при этом у нас остается выпуклым (отрезок [a,b] делит фигуру на два выпуклых многоугольника), а так как на контуре между a и b не лежало ни одной точки из S, то многоугольник все еще удовлетворяет требованиям задачи).
Итак, в качестве решения задачи мы получили выпуклую оболочку множества S (о построении ее см. задачу 10).
Если построенная выпуклая оболочка такова, что каждая точка S является ее вершиной (или лежит на стороне), то задача решена, иначе решения не существует.
[Назад]
Решение задачи 12.
Рассмотрим два из возможных алгоритмов.
Вариант 1. Строим выпуклую оболочку данного множества точек (см. задачу 10).
Если все точки множества A лежат на контуре, то задача решена. Если же нет, то ищем точку l с минимальным расстоянием до контура -- пусть это минимальное расстояние до стороны фигуры (u,v) (если таких точек несколько, то берем любую из них), вставляем в контур точку l (вместо контура
... u,v ...
будет
... u,l,v, ...).
Для оставшихся точек повторяем описанную выше процедуру, пока последняя не будет вставлена в контур.
Расстояние от точки до стороны - это либо длина перпендикуляра, опущенного из точки на сторону (если проекция точки попадает на отрезок, см. задачу 4), либо, в противном случае, минимальное из расстояний от точки до концевых точек стороны.
Расстояние от точки z(u,v) до ее проекции на прямую Ax+By+C=0 есть
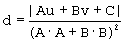
Вариант 2. Строим выпуклую оболочку V данного множества точек (см. задачу 10).
Если все точки множества A лежат на контуре, то задача решена. Иначе обозначим через A1 все внутренние точки выпуклой оболочки V. Строим для нового множества A1 выпуклую оболочку V1 (контуры V и V1 не пересекаются!).
"Склеиваем" два контура:
Выберем по паре последовательных вершин p,s и p1,s1 на контурах V и V1 соответственно так, чтобы в четырехугольнике с вершинами s,p,p1,s1 не лежало больше никаких других точек контуров V и V1. Разрываем контуры V и V1 (убирая ребра (p,s) и (p1,s1)) и объединяем их (добавляя ребра (p,p1) и (s,s1)).
Если внутри V1 нет внутренних точек, то задача решена, иначе же с внутренними точками V1 проделываем те же самые операции: находим выпуклую оболочку и пары последовательных точек на контурах, разрываем и склеиваем контуры, и т.д., пока не получим, что последняя построенная выпуклая оболочка содержит в себе 0, 1 или 2 точки.
Если точек 0, то задача решена. В противном случае присоединяем точки к ранее образованному контуру так, чтобы фигура осталась многоугольником (можно проводить присоединение, как и в варианте 1).
[Назад]
Решение задачи 13.
У клеточной фигуры (представьте себе, что в тетрадке Вы зарисовали на листе какое-то количество клеточек) могут быть следующие оси симметрии - горизонтальная, вертикальная и идущие под углом 45 и -45 градусов (т.е. 4 оси симметрии - как у квадрата). При любых других осях клетки листа при отображении не перейдут в клетки. Оси могут проходить как через центр какой-то клетки, так и по стороне. Например, фигуры
***
*** и ***
имеют по 2 оси симметрии - горизонтальную и вертикальную, а фигура * - все 4 оси симметрии.
Вводим систему координат таким образом, что каждая зарисованная клетка представляется точкой с целочисленными координатами.
Находим вероятный центр симметрии фигуры(имеющий координаты
((Xmax + Xmin)/2, (Ymax+Ymin)/2), где Xmax, Ymax, Xmin и Ymin соответственно максимальные и минимальные иксовые и игрековые координаты точек в заданной нами системе координат:
Xmax = max{Xi} ; Ymax = max{Yi},
Xmin = min{Xi} ; Ymin = min{Yi} ).
Если у фигуры есть ось симметрии, то она проходит через этот вероятный центр симметрии фигуры
Рассматриваем 4 возможных оси симметрии, проходящие через этот центр. Определяем, является ли фигура симметричной относительно каждой из осей. (Для удобства этот центр можно считать началом системы координат. При симметрии относительно горизонтальной (вертикальной) оси каждой клетке фигуры (x,y) должна соответствовать клетка с такой
же иксовой (игрековой) координатой, но с обратной по знаку другой координатой, т.е. (x,-y) (соответственно, для вертикальной оси (-x,y)). При симметрии относительно оси с наклоном 45 (-45) градусов каждой клетке (x,y) фигуры должна соответствовать клетка с координатой (y,x) (соответственно (-y,-x)).
[Назад]
Решение задачи 14.
Отрезки, соединяющие точки разбиения R1 и R2, параллельны стороне AD. Будем брать отрезки, соединяющие последовательные точки разбиения R3 и R4 и искать между этими двумя последовательными отрезками четырехугольник с наибольшей площадью. Четырехугольник разбиения Q с максимальной площадью есть четырехугольник с максимальной площадью по всем таким разбиениям прямоугольника отрезками.
Пусть последовательные точки разбиения с одинаковыми номерами
на сторонах BC и AD есть, соответственно f1,f2 и g1,g2.
Если f2-f1=g2-g1, то анализируемые четырехугольники есть параллелепипеды, и параллелепипед с максимальной площадью определяется максимальной длиной отрезка в разбиении R1 (или, что то же, R2).
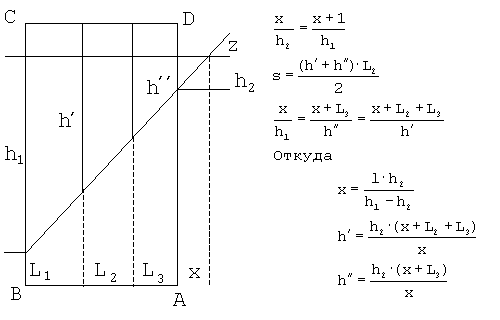 Если, для определенности f2-f1 > g2-g1 (случай обратного неравенства рассматривается аналогично), то, обозначая f2-f1=h1, g2-g1=h2, l=CD, h' и h" - соответственно высоты левой и правой сторон четырехугольника, L2 - ширину его основания, z - точку пересечения продолжения верхней и нижней сторон четырехугольника, L1, L3 и x - соответственно расстояния от левой стенки прямоугольника ABCD до четырехугольника, от правой стенки прямоугольника ABCD до четырехугольника, от точки x до прямоугольника ABCD, площадь четырехугольника - s; получаем следующую схему и равенства: Если, для определенности f2-f1 > g2-g1 (случай обратного неравенства рассматривается аналогично), то, обозначая f2-f1=h1, g2-g1=h2, l=CD, h' и h" - соответственно высоты левой и правой сторон четырехугольника, L2 - ширину его основания, z - точку пересечения продолжения верхней и нижней сторон четырехугольника, L1, L3 и x - соответственно расстояния от левой стенки прямоугольника ABCD до четырехугольника, от правой стенки прямоугольника ABCD до четырехугольника, от точки x до прямоугольника ABCD, площадь четырехугольника - s; получаем следующую схему и равенства:
Для каждой пары отрезков, определяемых точками разбиения R3 и R4, находим максимальную площадь четырехугольника между этими двумя отрезками.
[Назад]
Решение задачи 15.
Пусть координаты точек x1, ..., xN не убывают (если это не так, то просто отсортируем предварительно последовательность).
Метод решения #1.
Предположим, что мы нашли точку z, и она лежит на интервале (x[i],x[i+1]). Справа от нее i точек, слева - N-i. Сумма расстояний Smin будет такой:
Smin=(z-x[1])+ ... +(z-x[i])+(x[i+1]-z)+ ... +(x[N]-z).
Предположим, что i>N-i и мы в пределах интервала сдвигаем точку z влево на какую-то маленькую величину d (d<z-x[i]). Получаем новую сумму S
S=(z-d-x[1])+ ... +(z-d-x[i])+(x[i+1]-(z-d))+ ... +(x[N]-(z-d))=Smin-d*i+d*(N-i).
А так как, по предположению, i>N-i, то S<Smin !?
Ситуация, когда N-i>i, исследуется аналогично - мы делаем сдвиг на величину d<x[N+1] - z вправо, не выходя при этом за границы интервала, и опять же получаем, что новая сумма S<Smin. Случай, когда z совпадает с одной из точек x[i] исследуется так же, как и выше, используя маленькие сдвиги.
Следовательно, для того, чтобы точка z была искомой, необходимо и достаточно, чтобы справа и слева от нее лежало одно и то же число точек. Если N=2k, то точка z может быть любой из точек отрезка [x[k],x[k+1]], если же N=2k+1, то точка z=x[k+1].
Метод решения #2.
Пусть мы решаем задачу для N точек на прямой.
Точка z должна, очевидно, лежать на отрезке [x[1],x[N]].
Если N=1, то данная точка и является искомой.
Если N=2, то z может лежать где угодно на отрезке [x1,xN] - суммарное расстояние будет одинаковым и равным длине отрезка.
Если N>2, то суммарное расстояние от точки z до точек с минимальной и максимальной координатами (т.е. до точек x1 и xN) не зависит от местоположения точки z и равно длине отрезка [x1, xN]. Так как суммарное расстояние до этих двух точек постоянно, то поэтому мы можем их отбросить, и решать задачу уже для N-2 точек x2,...,xN-1. Проведя необходимое число раз сокращение количества точек, мы придем к уже рассмотренным случаям одной или двух точек.
Окончательно получаем: если N=2k, то точка z может быть любой из точек отрезка [xk,xk+1], если же N=2k+1, то точка z=x[k+1].
[Назад]
Решение задачи 16.
А) Единственный способ найти такую точку - это вычислить все суммы расстояний, а затем взять среди них минимальную. Расстояние между точками x(x1,x2) и y(y1,y2) считается по формуле
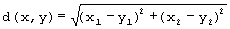 . .
Если же расстояние считается по формуле
d(x,y)=|x1-y1|+|x2-y2|,
то в этом случае применима идея решения задачи 15 (посмотрите, что и как тогда получается).
В) Z есть центр масс системы из N точек
Zx=(x1+ ... +xN)/N
Zy=(y1+ ... +yN)/N
[Назад]
Решение задачи 17.
Переформулируем задачу: На плоскости своими координатами задаются N точек Pi(xi,yi). Построить окружность минимального радиуса с центром на оси абсцисс так, чтобы она содержала внутри себя и на своей границе все эти точки.
Везде в дальнейшем будем обозначать через C(P,Z) окружность с центром в точке (P,O) и проходящую через точку Z=(Zx,Zy).
Очевидно, что на искомой окружности лежит по меньшей мере одна точка. Действительно, в противном случае мы можем, не меняя центра окружности, уменьшить ее радиус, а это противоречит предположению о том, что нами была построена окружность минимального радиуса.
Докажем следующее простое утверждение: Если на искомой окружности лежит единственная точка, то центр окружности есть проекция этой точки на ось абсцисс.
Предположим противное - на минимальной окружности лежит единственная точка Z(Zx,Zy), а центр ее не совпадает с (Zx,0). Если мы начнем понемножку двигать центр окружности, проходящей через точку Z, в направлении (Zx,0), то, так как все точки, кроме Z, лежат внутри окружности, до какого-то момента они и будут оставаться внутри нее. Таким образом мы можем хоть чуть-чуть, но сдвинуть центр, уменьшив при этом радиус окружности, содержащей все точки. Получаем противоречие с предположением о минимальности радиуса.
Следствие. Если на искомой окружности лежит только одна точка, то это точка с максимальной по модулю ординатой.
Отметим далее, что окружность с центром на оси абсцисс
единственным образом определяется двумя лежащими на ней точками (центр этой окружности - это точка пересечения оси абсцисс и срединного перпендикуляра к отрезку, соединяющего эти две точки).
Таким образом мы получаем следующий
Алгоритм 1:
Шаг 1.Ищем точку (xi,yi) с максимальной по модулю ординатой yi (если таких точек несколько, и у них разные абсциссы, то перейти на Шаг 2), и для окружности C(xi,(xi,yi)) проверяем, содержит ли она все N точек. Если да, то задача решена, если нет, то
Шаг 2. Среди окружностей, определяемых всевозможными парами точек (Pi, Pj), находим те, которые содержат все точки, а затем выбираем из них окружность минимального радиуса.
Пар точек, которые могут определять окружности, всего N(N-1)/2, т.е. порядка N*N, следовательно, и возможных окружностей тоже порядка N*N. Для проверки принадлежности N точек каждой окружности требуется порядка N операций. Получаем, что сложность этого алгоритма порядка N3. (Когда мы говорим о сложности алгоритма, то мы рассматриваем только зависимость роста числа требуемых операций от числа N, игнорируя все константные множители и медленно растущие слагаемые).
Рассмотрим другой способ решения этой задачи, основанный
на более глубоком ее анализе.
Вариант #2.
Проверка по Шагу 1 ранее изложенного алгоритма остается без изменения. Пусть искомая окружность не найдена.
Для обоснования Шага 2 докажем следующее утверждение: Пусть окружность с центром (Pij,0) определяется точками
Pi(xi,yi) и Pj(xj,yj). Она только тогда может быть содержащей все точки окружностью C минимального радиуса, когда (Pij,0) лежит на ортогональной проекции отрезка [(xi,yi),(xj,yj)] на ось абсцисс, т.е. должны выполняться неравенства xi<=Pij<=xj.
Окружность C с центром (Pij0) должна проходить не менее чем через 2 точки заданного множества из N точек, и при этом из этих точек всегда можно выбрать две такие (обозначим их Pi(xi,yi) и Pj(xj,yj)), что xi<Pij<xj. Действительно, если бы абсциссы всех лежащих на окружности точек были, например, меньше Pij, то (Pij,0) можно было бы сместить влево по оси абсцисс на некоторую величину с уменьшением радиуса охватывающей все точки окружности, что противоречит минимальности найденной ранее окружности.
Ни одна из точек, лежащих на окружности не может иметь абсциссы Pij вследствие невыполнения условия Шага 1.
Итак: всегда можно найти две лежащие на окружности точки Pi и Pj с абсциссами, соответственно, меньше и больше абсциссы центра окружности. Эти точки определяют центр окружности (Pij,0) - точку пересечение серединного перпендикуляра к отрезку [Pi,Pj] с осью абсцисс. При этом точка (Pij,0), естественно, будет лежать на проекции отрезка [Pi,Pj] на ось абсцисс.
Рассматривая все пары точек (Pi,Pj) таких, что точка пересечения (Pij,0) серединного перпендикуляра к отрезку [Pi,Pj] с осью абсцисс лежит на проекции отрезка [Pi,Pj] на ось абсцисс, получаем, что центр искомой окружности минимального радиуса совпадает с одной из таким образом полученных точек. Каждая из рассматриваемых пар точек (Pi,Pj) определяет окружность минимального радиуса Rij, содержащую эти две точки.
Из всего вышесказанного получаем, что интересующая нас окружность минимального радиуса, содержащая N точек, должна
иметь максимальный из всех полученных радиусов Rij.
Всего пар точек (Pi,Pj) не более (N2-N)/2, и, следовательно, сложность алгоритма
O((N2-N)/2) = O(N2-N) = O(N2).
Тут мы, как и обычно, избавляемся от констант и медленно растущих слагаемых.
Вариант #3.
Все вычисления на машине проводятся с ограниченной точностью, с определенным числом знаков после запятой. Поэтому нам бывает достаточно только указать, что интересующая нас точка лежит внутри отрезка заранее заданной длины epsilon. Epsilon задается пользователем. Например, если мы хотим найти координату точки с точностью 5 знаков после запятой, то epsilon = 10-6.
В отличие от варианта #2 мы не будем брать все перпендикуляры, попадающие на проекции отрезков и искать среди получаемых окружностей окружность с максимальным радиусом. Наоборот, описанным ниже способом будем выбирать точку на оси абсцисс и проверять, является ли она искомой или нет.
Из варианта решения #2 можно сделать вывод, что искомая точка лежит на отрезке [A0,B0]=[min{xi},max{xi}]. Пусть C0=(A0+B0)/2 - середина этого отрезка, а L=B0-A0 его длина.
Обозначим:
D1(C0)=максимальное из расстояний от точки (C0,0) до точек (xi,yi) с абсциссами xi<=C0;
Dr(C0)=максимальное из расстояний от точки (C0,0) до точек (xi,yi) с абсциссами xi>=C0.
i-ый итеративный (повторяющийся) шаг алгоритма, i=0, 1, 2, 3, ... :
Если Bi-Ai<=epsilon, то центр окружности лежит на отрезке [Ai,Bi] и желаемая точность достигнута. Стоп.
Иначе
Вычисляем Ci=(Ai+Bi)/2.
Находим Dl(Ci) и Dr(Ci).
Если Dl(Ci)<Dr(Ci), то искомая точка не может лежать на промежутке [Ai,Ci), так как радиус любой содержащей N точек окружности с центром на этом промежутке больше Dr(Ci) (проверьте сами!), а окружность с центром Ci имеет радиус Dr(Ci). Поэтому центр искомой окружности лежит на [Ci,Bi], который мы обозначим [Ai+1,Bi+1],
иначе, если Dr(Ci)<Dl(Ci), то, аналогично, получаем, что центр искомой окружности лежит на [Ai,Ci], которой мы обозначим [Ai+1,Bi+1]
иначе, если Dr(Ci)=Dl(Ci),
то Ci - центр искомой окружности. Стоп.
Конец i-го итеративного шага. Выполнить шаг i+1.
Мы видим, что длина L начального отрезка на каждом шаге уменьшается вдвое. Алгоритм, вообще говоря, заканчивает работу при выполнении условия
L/(2S)<=epsilon,
т.е. требуется не более чем S=[log2 (L/epsilon)]+1 шагов, где log2 - это логарифм по основанию 2.
Так как на каждом шаге (для вычисления Dl и Dr) выполняется не более O(N) операций, то всего их потребуется порядка O(N log2 (L/epsilon)).
[Назад]
Решение задачи 18.
Это переборная задача. Обратите внимание, что стороны квадрата могут и не быть параллельны осям координат! Каждую из N точек мы последовательно рассматриваем в качестве верхнего левого угла квадрата, каждую из оставшихся N-1 - как нижнюю правую вершины и смотрим, есть ли для них в этом множестве из N точек точки, соответствующие верхнему правому и нижнему левому углу. Если да, то подсчитываем, сколько точек лежат в данном квадрате.
Пусть координата левого верхнего угла (x1,y1), нижнего правого (x2,y2), тогда координата пересечения диагоналей четырехугольника ((x1+x2)/2,(y1+y2)/2); координата верхнего правого угла
((x1+x2)/2+[y1-(y1+y2)/2],(y1+y2)/2+[x1-(x1+x2)/2])= =((x1+x2+y1-y2)/2, (x1-x2+y1+y2)/2),
нижнего левого - ((x1+x2-y1+y2)/2,(-x1+x2+y1+y2)/2)
(Постройте чертеж и проверьте !).
Для (x1,y2) и (x2,y2) должны выполняться следующие неравенства: x1<=x2, y1>=y2 (иначе это будут уже не левый верхний и правый нижний углы квадрата).
Проверка принадлежности точки фигуре - см. задачу 8.
Программа:
{В исходном множестве поочередно перебираются все пары точек.}
{Предполагая, что отрезок, соединяющий эти точки, является ребром}
{квадрата строим квадрат и смотрим, все ли его вершины имеются в}
{исходном множестве. Если все, то определяем, сколько точек из}
{исходного множества лежит внутри этого квадрата. Если это число}
{превосходит старый рекорд то запоминаем найденный квадрат.}
{ }
{$A-,B-,D-,E+,F-,I+,L-,N-,O-,R-,S-,V-}
{$M 65520,0,655360}
uses crt;
const
maxn = 100;{ Максимальное число точек }
type
xy = record x,y : real end; { Тип для записи координат точек }
var
m : array[1..maxn] of xy; { Координаты точек множества }
i,j,g,k,n,p : word; { вспомогательные переменные }
num : word; { для записи числа точек в текущем квадрате }
rec : word; { для записи числа точек в лучшем квадрате }
a1,b1,c1 : real; { вспомогательные переменные }
r,c : array[1..5] of xy;{ для записи вершин квадратов }
f1,f2 : boolean;
o : array[1..4] of shortint;
Function sign(a : real) : shortint;{ Функция signum }
begin
if a<0 then sign:=-1
else if a>0 then sign:=1
else sign:=0
end;
{ нахождение коэффициентов прямой,
проходящей через точки x1,y1 и x2,y2 }
procedure getabc(x1,y1,x2,y2:real; var a,b,c:real);
begin
a:=y2-y1; b:=x1-x2; c:=-(a*x1+b*y1)
end;
begin
write('Введите число точек...'); readln(n);
for i:=1 to n do
begin
write('Введите координаты ',i,'-ой точки...');
readln(m[i].x,m[i].y); end;
rec:=0;{ Обнуление рекорда }
for i:=1 to n do
{ Перебор всех квадратов, для которых отрезок m[i]-m[j] }
for j:=1 to n do { является ребром }
if i<>j then
begin
c[1]:=m[i]; c[2]:=m[j];
{ Определение вершин квадрата }
c[3].x:=c[2].x+(c[1].y-c[2].y);
c[3].y:=c[2].y+(c[2].x-c[1].x);
c[4].x:=c[1].x+(c[1].y-c[2].y);
c[4].y:=c[1].y+(c[2].x-c[1].x);
c[5]:=c[1];
num:=0;
{ Проверка на наличие всех вершин квадрата
в исходном множестве точек }
f1:=false; f2:=false;
for g:=1 to n do
if (m[g].x=c[3].x) and (m[g].y=c[3].y) then f1:=true;
for g:=1 to n do
if (m[g].x=c[4].x) and (m[g].y=c[4].y) then f2:=true;
if (c[1].x=c[2].x) and (c[1].y=c[2].y) then f1:=false;
if f1 and f2 then
{Если все вершины квадрата есть в исходном множестве}
for k:=1 to n do { то определяем число точек в квадрате}
begin
for g:=1 to 4 do
begin
getabc(c[g].x,c[g].y,c[g+1].x,c[g+1].y,a1,b1,c1);
o[g]:=sign(a1*m[k].x+b1*m[k].y+c1);
end;
if ((o[1]=o[2]) and (o[2]=o[3]) and (o[3]=o[4])) or
((o[1]=o[2]) and (o[2]=o[3]) and (o[4]=0)) or
((o[1]=o[2]) and (o[2]=o[4]) and (o[3]=0)) or
((o[1]=o[3]) and (o[3]=o[4]) and (o[2]=0)) or
((o[2]=o[3]) and (o[3]=o[4]) and (o[1]=0)) or
((m[k].x=c[1].x) and (m[k].y=c[1].y)) or
((m[k].x=c[2].x) and (m[k].y=c[2].y)) or ((m[k].x=c[3].x)
and (m[k].y=c[3].y)) or ((m[k].x=c[4].x)
and (m[k].y=c[4].y)) then inc(num);
end;
if rec<num then begin r:=c; rec:=num end;
end;
if rec=0 then { Не найдено ни одного квадрата }
begin
writeln('Не найдено ни одного квадрата.'); halt
end;
{ Вывод результатов }
write('Лучший квадрат : ');
for i:=1 to 3 do write('(',r[i].x:2:2,[Назад]
Решение задачи 19.
На первом этапе на основании координат вершин прямоугольников формируем 4 массива: массив Х-овых координат вершин прямоугольника и связанный с ним массив номеров прямоугольников,вершина которого соответствует данной Х-овой координате;аналогично формируются массивы для У-овых координат. При этом координате вершины ставится в соответствие номер со знаком "+", если вершина левая нижняя, и знак "-", если правая верхняя.
На втором этапе массивы координат сортируются в порядке неубывания (при этом соответствие между координатами и вершинами сохраняется), причем для одинаковых координат вначале должны располагаться номера левых нижних вершин (т.е. со знаком "+"), а затем номера правых верхних. Это легко делается, если рассматривать номера как вторые значения для сортировки.
На следующих этапах проводится просмотр необходимых точек (будут рассмотрены все точки, лежащие на пересечении горизонтальных и вертикальных линий, проходящих через вершины прямоугольников) следующим образом. Формируется массив активных прямоугольников по У-овым координатам. Для этого, начиная с минимальной У-овой координаты, доходим до ближайшей координаты, у которой номер вершины имеет знак "-" или ее координата отлична от предыдущей координаты. При этом номера всех пройденных вершин активизируем. Для этого в массиве АКТИВНАЯ на соответствующее место ставим 1 или 0 (вначале все элементы массива равны 0). 1 ставится при прохождении вершины со знаком "+", 0- со знаком "-".
После поиска нужной У-овой координаты просматриваем все Х-овые координаты по такому же принципу, как при нахождении максимального пересечения отрезков (т.е. если встречаем вершину со знаком "+", то текущее количество пересечений увеличиваем на 1, а если встречаем вершину со знаком "-", то уменьшаем на 1). При этом
учитывается, активна ли встреченная вершина. Таким образом, изменение текущего количества пересечений выполняется только для активных вершин. После вычисления максимального значения пересечения для текущей У-овой координаты переходим к очередной У-овой координате. Описанные действия выполняются, пока все У-овые координаты не будут просмотрены.
[Назад]
Решение задачи 20.
Понятно, что если есть свеча с нулевыми координатами или две свечи лежат на прямой, проходящей через начало координат, по разные стороны от начала координат, то решения не существует. Пусть таких свеч нет.
Проведем линию через центр и первую свечу (пусть это точка А). Если все свечи оказались по одну сторону линии, то решение построено. Предположим, что существуют свечи по разные стороны прямой. Определим направление прямой от центра к свече, и пусть М - множество точек, лежащих по правую сторону от прямой. Определим среди них точку В, для которой угол АОВ максимальный и лежит в пределах от 0 до 180 градусов. Это можно определить через косинус угла АОВ ( большему углу соответствует меньший косинус). Проведя вторую линию ОВ, проверяем, лежат ли все свечи по одну сторону от нее. Если да, то решение найдено. Если нет, то решения нет.
[Назад]
Решение задачи 21.
Припишем сторонам каждого из N прямоугольников ориентацию: левая сторона считается идущей снизу вверх (ориентацию обозначим 1), верхняя - слева направо (2), правая - сверху вниз (3), нижняя - слева направо (ориентация 4). Найдем точки пересечения N прямоугольников. Обозначим это множество точек S. Добавим в S угловые точки всех прямоугольников. Каждой из точек S припишем пару, состоящую из двух ориентаций, соответствующих ориентациям тех ребер, пересечением которых точка является.
Найдем в множестве S точку с максимальной ординатой. Так как таких точек несколько, то возьмем среди них точку P0 с минимальной абсциссой. Эта точка лежит на верхней части контура объединения прямоугольников и является левым верхним углом какого-то прямоугольника. Печатаем P0. Будем двигаться от P0 вниз по ребру, пока не встретим одну из точек S (это будет либо точка - угол прямоугольника, либо точка - пересечение сторон). Обозначим эту точку P1. Ей приписана пара ориентаций (O1,O2), одна из ориентаций (пусть, например, O1) есть 3 (это то ребро, по которому мы пришли в P1). Печатаем P1 - очередную вершину контура, и двигаемся из точки P1 (по ребру какого-то прямоугольника) в направлении O2, пока не достигнем еще какой-нибудь вершины из S. Обозначим ее P2. У нее пара ориентаций (O1',O2'). Пусть, например, O2'=O2, тогда мы из очередной вершины контура P2 будем двигаться в направлении O1', и т.д., пока не достигнем вершины P0. Контур выписан.
Определим, есть ли в контуре "дырки". Занесем в массив A[1..2,1..2*N] в строку 1 все ординаты вершин прямоугольников без повторений и отсортируем этот массив по первой строке по возрастанию. Предположим, что в массиве A хранится всего S различных ординат: A[1,1], ... ,A[1,s]. Сначала все A[2,i]=0, i=1, ... , s.
Определим массив B[1..4,1..N]. В первой строке массива B располагаются в порядке неубывания x - координаты левых нижних и правых верхних вершин всех N прямоугольников:
B[1,i] - x - координата какой-то вершины P
B[2,i] и B[3,i] соответственно - ординаты нижней и верхней вершин той вертикальной стороны прямоугольника, на которой лежит P.
B[4,i]=0, если эта вертикальная сторона прямоугольника левая и 1, если правая.
Воспользуемся методом сканирующей прямой:
Будем брать по возрастанию индекса i элементы B[1,i] массива B, и увеличивать на 1 все элементы A[2,j] такие, что
B[2,i]<=A[1,j]<B[3,i] (A[2,j] будет равно количеству прямоугольни-
ков, содержащих внутри себя или на границе отрезок A[1,j]<=y<=A[2,j], x=B[1,i]). Если какое-то A[2,j]=0, то это означает, что прямоугольники при x=B[1,i] не покрывают интервал y=(A[1,j],A[1,j+1]).
Если мы найдем такие i,l и k, что при x=B[1,i] интервал (A[1,l],A[1,k+1]) не покрыт многоугольниками (т.е. A[2,l] = = A[2,l+1] = ... = A[2,k]=0), а интервалы (A[1,l-1], A[1,l]) и (A[1,k+1],A[1,k+2]) покрыты (т.е. A[2,l-1]>0 и A[2,k+1]>0), и точка (x,y)=(B[1,i],A[1,l]) не принадлежит внешнему контуру фигуры объединения прямоугольников, то у фигуры есть по крайней мере одна дырка. Чтобы, при необходимости, выписать контур дырки, поступим как и в случае нахождения внешнего контура - пойдем по ребрам, образующим контур.
Пункт 3 задачи решается перебором.
Для решения пункта 4 см. задачу 5.
[Назад]
Решение задачи 22.
Контур может иметь излом лишь в точках, соответствующих стенам зданий. Занесем в массив А координаты Li и Ri и отсортируем его по неубыванию. Заметим также, что между двух соседних стен (определяемых каждыми двумя соседними элементами массива) высота контура остается постоянной. Поэтому для каждых двух соседних элементов массива А найдем их полусумму (координату точки, лежащей между стенами) и вычислим высоту контура в этой точке; после этого мы будем знать высоты всех горизонтальных площадок и координаты начала и конца этих площадок. Будем выписывать контур точка за точкой, начиная с самой левой точки контура. Если две соседние горизонтальные площадки имеют одинаковую высоту, то мы их "склеиваем", т.е. рассматриваем как одну площадку. Если же две соседние площадки различаются по высоте, то, следовательно, надо выписать горизонтальный излом контура.
[Назад]
Решение задачи 23.
Считаем, что точки в S не дублируется (т.к. S - множество). Введем в множество S точки (0,W),(0,0),(V,0),(V,W) - вершины A.
Пусть есть два двумерных массива - BX и BY; в массиве BX
располагаются координаты точек множества S в порядке неубывания абсциссы, в BY - по невозрастанию ординаты. Будем считать, что BX[i,1] и BX[i,2] (аналогично BY[j,1] и BY[j,2]) соответственно x и y-координаты точки из S.
Рассмотрим множество прямоугольников Pi, удовлетворяющих условию задачи. Тот из них, который имеет максимальную площадь и является искомым. Очевидно, что на каждой из сторон Pi должна лежать точка из S, либо сторона Pi должна лежать на стороне A.
Рассмотрим следующие случаи:
1) Верхняя сторона P лежит на верхней стороне прямоугольника A. Для каждой точки BX[i] ищем, двигаясь по массиву BX вправо и влево от элемента BX[i] такие первые BX[j] и BX[k], j<i, k>i, что BX[j,2]>BX[i,2], BX[k,2]>BX[i,2].
Считаем, что стороны прямоугольника Pi проходит: нижняя - через точку BX[i], левая - через BX[j], правая - через BX[k]. Верхняя сторона лежит на верхней стороне A.
Таким образом находим все прямоугольники, примыкающие к верхней стороне.
Прямоугольники, примыкающие к нижней, левой и правой сторонам A находятся аналогично, но в двух последних случаях надо вместо BX использовать массив BY.
2) Случай, когда ни одна из сторон Pi не лежит на стороне A. Берем последовательно точки массива BY[i], i=1, ..., N, и считаем, что верхняя сторона Pi проходит через точку BY[i]. Для этой точки полагаем сначала, что XBegin=0, XEnd=V. Находим такие точки BY[j] и BY[k] (при просмотре массива BY вправо от элемента BY[i]), что BY[j,2]<BY[i,2], BY[k,2]<BY[i,2], BY[j,1]<=XBegin, BY[k,1]<=XEnd, BY[j,1]<BY[i,1], BY[k,1]>BY[i,1] (объяснение смотрите ниже), т.е. мы находим точки с максимальной ординатой, через которые можно провести правую и левую стороны прямоугольника Pi). Внутри интервала (BY[j,1], BY[k,1]) на оси OX ищем точку BY[l,1] такую, что y - координата этой точки BY[l,2] максимальная, меньшая величины max{BY[j,2],BY[k,2]}.
Через эту точку BY[l] будем проходить нижняя сторона прямоугольника. Полагаем XBegin=BY[j,1], XEnd=BY[k,1].
Но этим прямоугольником может не исчерпываться все множество прямоугольников, у которых точка BY[i] лежит на верхней стороне. Попытаемся найти еще один из таких прямоугольников. Очевидно, что левая его сторона имеет x-координату не меньшую, чем XBegin, а правая - не большую, чем XEnd. Будем искать такую точку BY[l], что XBegin<=BY[l,1]<=XEnd (теперь уже понятно почему), BY[l,2] максимальная из всех ординат, меньших max{BY[j,2],BY[k,2]} (мы "сужаем" прямоугольник как можно незначительнее). Если BY[l,1]<BY[i,1], то это новая левая сторона, иначе - новая правая. Находим новую нижнюю сторону, и т.д. Если мы не можем найти нового BY[l], то просмотр прямоугольников с точкой BY[i] на верхней стороне закончен, и мы переходим к BY[i+1].
[Назад]
Решение задачи 24.
Длина стороны первого квадрата - 1, второго - 1, третьего 2, четвертого - 3, и т.д. Видно, что длины сторон есть числа Фибоначчи, определяемые следующим рекуррентным соотношением
u1=1, u2=1, uN=uN-1+uN-2.
Будем хранить координаты четырехугольника Ai - объединения квадратов с номерами от 1 до i.
Второй квадрат рисуется справа от первого (A1),
третий - сверху от A2,
четвертый - слева от A3, пятый - снизу от A4,
шестой - опять справа от A5 и т.д.
Как только точка P впервые попадает в Ai, мы распечатываем номер i.
Проверка принадлежности точки P четырехугольнику с параллельными осям сторонами:
Пусть левый верхний угол (x1,y1), правый нижний (x2,y2). Точка P(Px,Py) принадлежит четырехугольнику, если одновременно x1<=Px<=x2 и y2<=Py<=y1.
[Назад]
Решение задачи 25.
Отсортировав координаты точек в порядке неубывания Х-овых координат, а в случае одинаковых Х-овых координат в порядке неубывания У-овых координат, находим координаты средней точки (находящуюся в позиции n div 2+1), пусть это точка (Х0,У0). При этом множество точек оказалось разбито на 3 части: точки, лежащие на прямой х=Х0; точки, лежащие левее прямой х=Х0; точки, лежащие правее прямой х=Х0. Представим, что точки, лежащие левее прямой х=Х0 ( точки, лежащие правее прямой х=Х0) лежат в пределах некоторого прямоугольника, где Х1 (Х2) координаты его правого (левого) края. Тогда легко понять, что существует прямая с достаточно большим углом наклона, которая разделяет эти части. Осталось разделить только точки на прямой, чтобы количество точек в получившихся частях было соответствующим (т.е. пересечение прямой с прямой х=Х0). Если количество точек нечетно, то искомая линия проходит через среднюю точку, иначе над средней точкой (но под предыдущей, если она лежит па прямой х=Х0).
Определим:
Х1 - может быть легко найдена просмотром массива Х-овых координат справа налево от средней точки до нахождения первой координаты, отличной от Х0. Если такая координата не найдена, то Х1=Х0-1.
Х2 - может быть легко найдена просмотром массива Х-овых координат слева направо от средней точки до нахождения первой координаты, отличной от Х0. Если такая координата не найдена, то Х1=Х0+1.
У1 - это У-овая координата точки, предшествующей средней точке, если Х-ая ее координата равна Х0, или равна У0-1, если Х-овая координата точки, предшествующей средней точке, не равна Х0.
После того, как Х0,У0,Х1,У1 найдены, осталось написать уравнение прямой через точки с координатами (Х2,У2) (Х3,У3), определяемыми по следующему правилу:
если N - четно
то Х2=Х0; У2=(У0+У1)/2, Х3=Х0+Z/2,У3=У0-Ymax+Ymin
иначе Х2=Х0; У2=У0, Х3=Х0+Z/2,У3=У0-Ymax+Ymin
где Ymax- максимальная У-овая координата, Ymin - минимальная У-овая координата, Z=min(Х0-Х1,Х2-Х0).
[Назад]
Решение задачи 26.
Проведем через каждую вершину этих двух выпуклых многоугольников параллельные оси Oy прямые. Эти прямые разбивают всю плоскость на сектора. Пересечение каждого сектора с выпуклым многоугольником образует трапецию. Поэтому внутри каждого сектора пересечением двух выпуклых многоугольников будет пресечение двух четырехугольников. Собираем все эти пересечения в одну фигуру, удаляя при этом ложные вершины, которые возникают на границах между секторами.
Объединение делается аналогично.
[Назад]
Решение задачи 27.
Если проекция точки Z попадает на сторону многоугольника, а не на ее продолжение (см. задачу 4), то минимальное расстояние от точки Z до стороны есть длина проведенного перпендикуляра. Если же проекция точки Z попадает на продолжение стороны, то минимальное расстояние есть минимум из расстояний от Z до концевых точек этой стороны.
Минимальное расстояние от точки Z до контура есть минимум из расстояний от точки Z до каждой из сторон.
[Назад]
Решение задачи 28.
Проверяем, лежит ли точка z на каком-либо отрезке. Если нет, то проводим отрезок, концевые точки которого z и, например, вершина 1. Находим ближайшую к z точку пересечения этого отрезка и сторон многоугольников, на которые разбивается плоскость. Пусть эта точка принадлежит стороне ab. Для этой стороны сначала определяем направление обхода (см. задачу 3); затем ищем следующую, смежную с текущей, сторону bc контура, которая образует минимальный по величине угол с отрезком ba (угол отсчитывается от отрезка ab по часовой или против часовой стрелки в зависимости от того, по или против часовой стрелки обход, сравнение углов - см. задачу 1). Находим замкнутый контур и определяем, находится ли точка z внутри него или снаружи. Если снаружи, то удаляем из фигуры все ребра этого контура и повторяем процесс.
Пример:
[Назад]
Решение задачи 29.
Подобные многоугольники могут быть зеркально симметричны! Фигура на плоскости полностью характеризуется матрицей расстояний С(i,j), С(i,j)=расстоянию от вершины i до вершины j. Для каждой из введенных фигур строим свою матрицу расстояний и проверяем, можем ли мы получить из одной матрицы вторую перестановкой строк и столбцов и умножением всех элементов матрицы на одно и то же число.
[Назад]
Решение задачи 30.
Дадим другую интерпретацию этой задачи: Есть N отрезков, описываемых уравнениями
ai*x+bi=y, x0<=x<=x1, i=1, ... ,N.
Предположим, что отрезки не совпадают.
1. Найти верхний контур объединения фигур
ai*x+bi<=y, i=1, ..., N, x0<=x<=x1,
(т.е. найти такую разбивку t0, ..., tp отрезка [x0,x1] и те кусочки отрезков ai*x+bi=y, tj<=x<=tj+1, j=1, ..., p, что отрезок ai*x+bi лежит не ниже любого другого отрезка al*x+bl при tj<=x<=tj+1)
2. Найти такую разбивку отрезка [x0,x1] точками Sj, что в каждом секторе Si<x<Si+1 кусочки отрезков ai*x+bi, i=1, ..., N не пересекаются, а на границах сектора, при x=Si и при x=Si+1, лежит по крайней мере по одной точке пересечения отрезков ai*x+bi, i=1,..., N.
Решим сначала пункт 2 задачи, затем пункт 1.
Найдем все точки пересечения отрезков ai*x+bi, i=1,...,N друг с другом. Добавим в это множество точки x0 и x1. Упорядочим точки пересечения по возрастанию (если в последовательности встречаются несколько точек с одним и тем же значением, то оставляем из них только одну). Получаем таким образом последовательность S0, ..., SQ.
Для каждого отрезка [Si, Si+1] находим его середину
Zi=(Si+Si+1)/2, вычисляем значения fj=aj*Zi+bj, j=1, ...,N, сортируем их по возрастанию. Индексы j значений fj в отсортированной последовательности - это как раз и есть искомая перестановка (i1,i2,...,iN) чисел 1,2,3, ..., N, упомянутая в формулировке задачи в пункте 2.
Для решения пункта 1 выпишем по порядку для каждого отрезка [Sj,Sj+1], j=0, ..., Q-1, величины iN (это индекс самого верхнего отрезка в секторе [Sj,Sj+1]). Отрезок с номером k может быть самым верхним для нескольких смежных секторов [Sj,Sj+1], ..., [Sl,Sl+1]. Поэтому мы просматриваем номера iN, соответствующие отрезкам [Sj,Sj+1], j=0, ..., Q-1 и определяем последовательные максимальные отрезки, помеченные одним и тем же номером. Концевые точки этих максимальных отрезков и есть искомые точки t0, ..., tp (они выбираются по указанному выше методу из точек S0, ..., SQ).
[Назад]
Решение задачи 31.
Прямая ax+by+c=0, проходящая через точки P(x1,y1) и S(x2,y2), должна удовлетворять равенствам
a*x1+b*y1+c=0 (1)
a*x2+b*y2+c=0 (2)
Вычитая из (1) уравнение (2), получаем
b/a=(x1-x2)/(y1-y2).
Если прямые параллельны, то их коэффициенты при x и y пропорциональны.
Для каждых двух точек множества A находим отношение коэффициентов b/a проходящей через эти точки прямой L. Находим число прямых множества B с тем же отношением коэффициентов (это - прямые, параллельные L).
[Назад]
Решение задачи 32.
Пусть в фигуре уже проведены L диагоналей, и они разбивают n-угольник на k частей. Проведем еще одну, L+1-ю диагональ. Подсчитаем, сколько ранее проведенных диагоналей пересекает во внутренних точках эта диагональ. Обозначим количество пересечений через S. Проведение диагонали
1) увеличивает количество разбивок n-угольника на 1;
2) каждое пересечение этой диагонали с ранее проведенной диагональю также увеличивает количество разбивок на 1 (по условию никакие 3 диагонали не пересекаются в одной точке).
Итак, после проведения диагонали L+1 количество частей K+S+1 (предполагается, что L+1-я диагональ не совпадает ни с одной ранее проведенной).
Как определить, пересекается ли диагональ, соединяющая вершины i и j, с диагональю, заданной вершинами k и l? Вершины i и j разбивают контур многоугольника на 2 части: множество A - вершины, лежащие на контуре между вершинами i и j, и множество B - вершины контура между j и i (множества A и B не включают i и j). Если K принадлежит одному из этих множеств, а L - другому, то диагонали пересекаются, иначе - нет.
[Назад]
Решение задачи 33.
Будем обозначать через Vi вершину ломаной с координатами (xi,yi).
Сначала рассмотрим разрез круга ломаной, состоящей только из двух ребер R1=(V1,V2) и R2=(V2,V3). Для того, чтобы разнять этот круг, необходимо тянуть в направлении вектора S, выходящего из точки V2 и лежащего либо внутри угла V1 V2 V3 (вершина угла -- точка V2), либо внутри центральносимметричного ему относительно точки V2 угла. Будем говорить, что вектор S лежит в конусе C2 с вершиной V2.
Аналогично, если ломаная определяется k вершинами, то для каждой пары ребер (Vi,Vi+1) и (Vi+1,Vi+2), i=1, ..., k-2, определяем конус Ci+1 возможных направлений перемещения, затем считаем, что параллельным переносом вершины всех конусов совмещены в одной точке. Пересечение всех Ci, i=2,...,k-1, и даст искомое возможное направление разнимания круга. Если это пересечение пусто, то круг разнять нельзя, иначе - можно.
[Назад]
Решение задачи 34.
Перебираем все возможные комбинации из трех точек, не лежащих на одной прямой. Находим, используя алгоритм решения задачи 2, искомый треугольник.
[Назад]
Решение задачи 35.
Считаем, что начало координат - это юго-восточный угол дома, и оси направлены параллельно стенам.
Сначала надо проверить, не попал ли после перемещений человек вовнутрь дома (проверка корректности входных данных). Если нет, то в случае, если человек находится в зоне x>=0, 0<=y<=5, то он видит только восточную стену дома; если в зоне x>=0,y>=5, то северную и восточную стены дома и т.д.
Другой способ решить эту задачу - определить, как в задаче 27 минимальное расстояние от человека до дома. Если минимум есть расстояние до угла дома, то человек видит две примыкающие к этому углу стороны, иначе - только ту сторону, расстояние до которой минимально.
[Назад]
Решение задачи 36.
Пусть точка z - центр координат (если это не так, сделаем параллельный перенос). Для того, чтобы звено забора было полностью видно, необходимо и достаточно, чтобы из точки z, где стоит человек, были видны обе вершины этого звена, и еще какая-нибудь его внутренняя точка. Будем считать, что вершина l звена видна, если интервал (z,l) не пересекает никаких звеньев забора, или же если обе концевые вершины пересекаемого звена k лежат на [z,l], т.е. человек смотрит вдоль звена k.
Отсортируем по неубыванию углы, образуемые с осью OX отрезками, одна концевая точка которых z, а вторая пробегает все вершины звеньев (углы отсчитываются от точки z в положительном направлении, т.е. против часовой стрелки). Получаем последовательность углов a1,a2, ,,, ,an. Добавляем в эту последовательность угол an+1=a1. Из точки z в направлении между прямыми, идущими под углами Li и Li+1 может быть виден кусок только одного единственного звена.
Из точки z под углами (ai+ai+1)/2, i=1, ... ,n, проводим лучи и для каждого луча смотрим, какое звено k этот луч пересекает первым (если первое пересечение происходит по вершине, то оно не рассматривается). В том случае, если у звена k видны обе вершины, то звено видно полностью, если хотя бы одна вершина не видна, то k видно частично.
После анализа точек пересечения всех n лучей те звенья, которые не видны ни полностью, ни частично, получают пометку невидимых.
[Назад]
Решение задачи 37.
Рассматриваем нумерацию граней как элементы массивов. Сортируем каждый из массивов с помощью некоторого обменного алгоритма (например, с помощью "пузырьковой" сортировки), подсчитывая количество обменов (пусть KN и KM). Если отсортированные массивы совпадают и (KN-KM) кратно 2, то тетраэдры совпадают. (Обмен двух граней можно трактовать как отражение тетраэдра в зеркале).
[]
|