Предварительные сведения.
Что такое граф?
Часто в задачах встречается следующая конструкция - есть дома и дороги, их соединяющие; у каждой дороги есть длина. По другой терминологии такая конструкция называется графом, дома называются "вершинами", дороги - "ребрами" или "дугами", а длина дороги "весом ребра" или "весом дуги". Таким образом фраза 'Найти минимальный вес пути между вершинами s и k в графе' может быть переведена так: 'Есть дома и дороги их соединяющие. Также заданы длины дорог. Найти кратчайшую длину пути от города s до города k, если двигаться можно только по дорогам'. Пропускная способность дуги (i,j) означает, например, сколько груза может быть перевезено по дороге (по дуге) (i,j) за единицу времени); а поток по дуге (i,j) -- это сколько перевозится сейчас на самом деле).
Часто используют следующие обозначения: Г(x(i))- множество вершин, в которые есть дуга из вершины i; Д(x(i))- множество вершин, из которых есть дуга в вершину i.
Пусть в графе N вершин.
Длины дуг обычно заносятся в матрицу (назовем ее C) размера N на N, называемой матрицей смежности:
var С: array [1..N,1..N] of integer;
Элемент C[i,j] этой матрицы равен длине дуги (дороги>), соединяющей вершины i и j, и равен (например) 0 или -1, если такой дуги нет. Если дорога двунаправленная (дуга неориентированная), то очевидно, что C[i,j]=C[j,i].
Алгоритм расстановки пометок для задачи о максимальном (от s к t) потоке.
А. Расстановка пометок. Вершина может находиться в одном из трех состояний: вершине приписана пометка и вершина просмотрена ( т.е. она имеет пометку и все смежные с ней вершины "обработаны"), пометка приписана, но вершина не просмотрена ( т.е. она имеет пометку, но не все смежные с ней вершины обработаны), вершина не имеет пометки. Пометка произвольной вершины x(i) состоит из двух частей и имеет один из двух видов: (+x(j),m) или (-x(j),m). Часть +x(j) пометки первого типа означает, что поток допускает увеличение вдоль дуги (x(j),x(i)). Часть -x(j) пометки другого типа означает, что поток может быть уменьшен вдоль дуги (x(i),x(j)). В обоих случаях m задает максимальную величину дополнительного потока, который может протекать от s к x(i) вдоль построенной увеличивающей цепи потока. Присвоение пометки вершине x(i) соответствует нахождению увеличивающей цепи потока от s к x(i). Сначала все вершины не имеют пометок.
- Шаг 1.
Присвоить вершине s пометку (+s,m(s)=бесконечность). Вершине s присвоена пометка и она просмотрена, все остальные вершины без пометок.
- Шаг 2.
Взять некоторую непросмотренную вершину с пометкой; пусть ее пометка будет (+-x(k),m(x(i))) (+- обозначает, что перед x(k) может стоять как плюс, так и минус).
(I) Каждой помеченной вершине x(j), принадлежащей Г(x(i)), для которой c(i,j)<q(i,j), присвоить пометку (-x(i),m(x(j))), где
m(x(j))=min[m(x(i)),q(i,j)-c(i,j)].
(II) Каждой непомеченной вершине x(j), принадлежащей Д(x), для которой c(i,j)>0, присвоить пометку (-x(i),m(x(j))), где
m(x(j))=min[m(x(i)),c(j,i)].
(Теперь вершина x(i) и помечена, и просмотрена, а вершины x(j), пометки которым присвоены в (I) и (II), являются непросмотренными.) Обозначить каким-либо способом, что вершина x(i) просмотрена.
- Шаг 3.
Повторять шаг 2 до тех пор, пока либо вершина t будет помечена, и тогда перейти к шагу 4, либо t будет не помечена и никаких других пометок нельзя будет расставить; в этом случае алгоритм заканчивает работу с максимальным вектором потока c. Здесь следует отметить, что если X(0)-множество помеченных вершин, а X'(0) - множество не помеченных, то ( X(0) --> X'(0) ) является минимальным разрезом.
Б. Увеличение потока.
- Шаг 4.
Положить x=t и перейти к шагу 5.
- Шаг 5.
(I) Если пометка в вершине x имеет вид (+z,m(x)), то изменить поток вдоль дуги (z,x) c c(z,x) на c(z,x)+m(t). (II) Если пометка в вершине x имеет вид (-x,z) c c(x,z) на c(x,z)-m(t).
- Шаг 6.
Если z=s, то стереть все пометки и вернуться к шагу 1, чтобы начать расставлять пометки, но используя уже улучшенный поток, найденный на шаге 5. Если z<>s, то взять x=z и вернуть к шагу 5.
Обозначения: Г(x(i))- множество вершин, в которые есть дуга из вершины i; Д(x(i))- множество вершин, из которых есть дуга в вершину i; c(i,j) - это пропускная способность дуги (т.е., например, сколько груза может быть перевезено по дороге (по дуге) (i,j) за единицу времени); q(i,j) - поток по дуге (i,j) (т.е. сколько перевозится сейчас на самом деле).
Кратчайшее расстояние от вершины нач до остальных вершин.
(Алгоритм Дейкстры).
Обозначения:
C[i,j]- длина ребра(i,j), С[i,j]>=0 (если ребра нет, то его длина полагается равной бесконечности).
D[i]- кратчайшее текущее расстояние от вершины нач до вершины i.
флаг[i]- информация о просмотре вершины i: 0 - если вершина не просмотрена, 1 - если просмотрена. Если вершина просмотрена, то для нее D[i] есть наикратчайшее расстояние от вершины нач до вершины i.
предок[i]- информация о номере вершины, предшествующей вершине i в кратчайшем пути от вершины нач.
минрас - это минимальное расстояние.
Алгоритм:
для i от 1 до N выполнять
нц
предок[i]:=нач;
флаг[i]:=0;
D[i]:=C[нач,i]
кц
флаг[нач]:=1; {пока мы знаем только расстояние}
предок[нач]:=0 {от вершины нач до нее же, равное 0}
для i от 1 до N-1 выполнять
нц
минрас:=бесконечность;
для j от 1 до N выполнять
если (флаг[j]=0 и (минрас > D[j]) {находим минимальное}
то минрас:=D[j]; {расстояние}
k:=j; {до непомеченных вершин}
все
флаг[k]:=1; {вершина k помечается просмотренной}
для j от 1 до N выполнять {выполняем просмотр}
если флаг[j]=0 и D[j]>D[k]+C[k,j]
{Т.е. если для вершины j еще не найдено кратчайшее расстояние
от нач, и из вершины k по дуге C[k,j] путь в j короче,
чем найденный ранее}
то D[j]:=D[k]+C[k,j] {то запоминаем его}
предок[j]:=k;
все
кц
Задача 1.
Задан набор неповторяющихся пар (Ai,Aj), Ai, Aj принадлежат множеству А={A1, A2, ..., An}. Необходимо составить цепочку максимальной длины по правилу
(Ai,Aj)+(Aj,Ak)=(Ai,Aj,Ak).
При образовании этой цепочки любая пара может быть использована не более одного раза.
[Решение]
Задача 2.
Между N пунктами (N<=50) заданы дороги длиной A(i,j), где I,J-номера пунктов. Дороги проложены на разной высоте и пересекаются только в общих пунктах. В начальный момент времени из заданных пунктов начинают двигаться с постоянной скоростью M роботов (M=2 или 3), независимо меняя направление движения только в пунктах. Роботы управляются таким образом, чтобы минимизировать время до встречи всех роботов в одном месте. Скорость I-того робота может быть равна 1 или 2. Остановка роботов запрещена.
Задание:
Написать программу, которая:
1) при заданных N,M и сети дорог единичной длины (все имеющиеся A(i,j)=1) определяет минимальное время, через которое может произойти встреча всех M роботов, при этом начальное положение роботов и скорость их движения известны.
2) Выполнить те же действия, что и в п. 1, но только для различных значений A(i,j).
Примечание: В случае невозможности встречи всех M роботов в одном месте ни в какой момент времени в результате выполнения программы должно быть сформировано соответствующее сообщение.
Требование к вводу-выводу:
1) Все входные данные - целые неотрицательные числа;
2) при задании сети дорог должно быть указано количество дорог - K и пункты их начала и конца в виде пар (i,j).
[Решение]
Задача 3.
На плоскости расположено N точек. Имеется робот, который двигается следующим образом. Стартуя с некоторой начальной точки и имея некоторое начальное направление, робот движется до первой встреченной на его пути точки, изменяя в ней свое текущее направление на 90 градусов, т.е. поворачивая налево или направо. После этого он продолжает движение аналогично. Если робот достиг начальной точки, либо не может достичь новой точки (которую он еще не посещал), то он останавливается.
Определить, может ли робот посетить все N точек, если:
- Определены начальные точка и направление робота.
- Определена начальная точка, а направление робота можно выбирать.
- Начальную точку и направление робота можно выбирать.
Координаты точек - целые числа, угол измеряется в радианах относительно оси ОХ.
[Решение]
Задача 4.
"ПУТЬ".
Найти кратчайшее расстояние между двумя вершинами в графе. Найти все возможные пути между этими двумя вершинами в графе не пеpесекающиеся по
а) pебpам
б) веpшинам.
[Решение]
Задача 5.
Лабиринт задается матрицей смежности N*N, где C(i,j)=1, если узел i связан узлом j посредством дороги. Часть узлов назначается входами, часть - выходами. Входы и выходы задаются последовательностями узлов X(1),..,X(p) и Y(1),..,Y(k) соответственно.
Найти максимальное число людей, которых можно провести от
входов до выходов таким образом, чтобы:
а) их пути не пересекались по дорогам, но могут пеpесекаться по узлам;
б) их пути не пересекались по узлам;
[Решение]
Задача 6.
N шестеpенок пpонумеpованы от 1 до N (N<=10). Заданы M (0<=M<=45) соединений паp шестеpенoк в виде (i,j), 1<=i<j<=N (шестеpня с номеpом i находится в зацеплении с шестеpней j). Можно ли повеpнуть шестеpню с номеpом 1?
Если да, то найти количество шестеpен, пpишедших в движение.
Если нет, то тpебуется убpать минимальное число шестеpен так, чтобы в оставшейся системе пpи вpащении шестеpни 1 во вpащение пpишло бы максимальное число шестеpен. Указать номеpа убpанных шестеpен ( если такой набоp не один, то любой из них ) и количество шестеpен, пpишедших в движение.
[Решение]
Задача 7.
На фигуре 1.показана вычислительная система, содержащая достаточное количество процессоров, использующих общую память из 26 числовых переменных A,B,C,....,Z. Система работает шагами. На каждом шаге, каждый процессор выполняет либо оператор присваивания либо пустой оператор. Оператор присваивания - это конструкция вида
(переменная)=(арифметическое выражение)
где арифметическое выражение без скобок и содержит не более 2 переменных и арифметические операции. Процессоры вычисляют выражения и присваивают их значения переменным из левых частей операторов, а потом приступают к следующим операторам (при том одновременно). Не допускается одновременное выполнение 2 или больше операторов присваивания с одинаковой левой частью. Пустой оператор обозначаем символом &. Выполняя его, процессор простаивает 1 шаг.
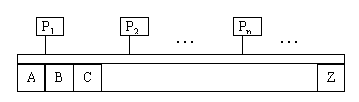
Фиг. 1
n последовательности операторов (присваивания или пустых) с одинаковой длиной L называем n-программой с длиной L (выполняется за L шагов на первых n процессоров), если на каждом шаге имеем не более 1 оператора с заданной левой частью. n-программы P и Q называем эквивалентными, если начиная с одного и того же начального состояния переменных A,B,...,Z после выполнения как P, так и Q получается одинаковый результат.
Напишите программу, которая:
Задание 1. Вводит целое k(k<25) и 1-программу, содержащую k операторов присваивания.
Задание 2. Проверяет правильность введенных операторов. Задание 3. Преобразует 1-программу в эквивалентную m-программу c минимальной длиной (добавляя если надо пустые операторы) и выводит полученный результат.
Задание 4. Не увеличивая длину построенной в Задании 3 n-программы, преобразует ее в эквивалентную m-программу, m-как можно меньше, и выводит полученный результат.
Замечание. На фигуре 2 показана 1-программа из 6 операторов и 3-программа и 2-программа - возможные решения задач 3(б) и 4(в).
|
a) |
D=A*D |
б) |
A=B+C |
B=C+D |
D=D-E |
|
A=B+C |
|
A=A-E |
& |
& |
|
A=A-E |
|
E=A*B |
D=A*D |
& |
|
B=C+D |
в) |
A=B+C |
B=C+D |
|
|
D=D-E |
|
A=A-E |
D=D-E |
|
|
E=A*B |
|
E=A*B |
D=A*D |
|
Фиг. 2
Задача 8.
Имеется N прямоугольных конвертов и N прямоугольных открыток различных размеров. Можно ли разложить все открытки по конвертам, чтобы в каждом конверте было по одной открытке.
Замечание. Открытки нельзя складывать, сгибать и т.п., но можно помещать в конверт под углом. Например, открытка с размерами сторон 5:1 помещается в конверты с размерами 5:1, 6:3, 4.3:4.3, но не входит в конверты с размерами 4:1, 10:0.5, 4.2:4.2.
[Решение]
Задача 9.
Составить программу для нахождения произвольного разбиения 20 студентов на 2 команды, численность которых отличается не более чем в 2 раза, если известно, что в любой команде должны быть студенты, обязательно знакомые друг с другом. Круг знакомств задается матрицей (20,20) с элементами
A(ij)={1,если i студент знаком с j
{0,иначе .
[Решение]
Задача 10.
Имеется N человек и прямоугольная таблица А[1:N,1:N];элемент A[i,j] равен 1, если человек i знаком с человеком j, А[i,j] = =А[j,i]. Можно ли разбить людей на 2 группы, чтобы в каждой группе были только незнакомые люди.
[Решение]
Задача 11.
На олимпиаду прибыло N человек. Некоторые из них знакомы между собой. Можно ли опосредованно перезнакомить их всех между собой? (Незнакомые люди могут познакомиться только через общего знакомого).
[Решение]
Задача 12.
Пусть группа состоит из N человек. В ней каждый имеет (N/2) друзей и не больше K врагов. У одного из них есть книга, которую все хотели бы прочитать и потом обсудить с некоторыми из остальных.
Написать программу, которая:
1. Находит способ передачи книги таким образом, чтобы она побывала у каждого в точности один раз, переходя только от друга к другу и наконец возвратилась к своему владельцу.
2.Разбивает людей на S групп, где будет обсуждаться книга, таким образом, чтобы вместе с каждым человеком в ту же самую группу вошло не более P его врагов.
Примечание: предполагается, что S*P>=K.
[Решение]
Задача 13.
В заданном графе необходимо определить, существует ли цикл, проходящий по каждому ребру графа ровно один раз.
[Решение]
Задача 14.
Следующая фигура показывает запутанную сеть дорог района города. Представьте, что мусорная машина должна пройти по всем дорогам хотя бы один раз, чтобы собрать мусор. Число на каждой стороне показывает время, которое должна потратить мусорная машина, чтобы проехать этот интервал. На перекрестках машина должна ждать время, равное числу пересекающихся дорог.
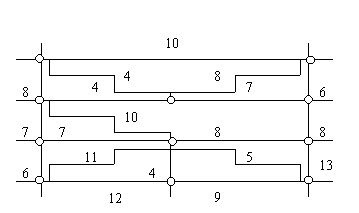
Составьте программу, показывающую как выбрать необходимый путь для сбора мусора в кратчайшее время.
Есть 11 остановок.
от 1 до 2 путь 10 мин.
от 1 до 3 4
от 1 до 4 8
от 2 до 3 8
от 2 до 5 6
от 3 до 4 4
от 3 до 5 7
от 4 до 7 7
от 4 до 6 10
от 4 до 8 7
от 8 до 6 7
от 8 до 10 6
от 10 до 6 11
от 6 до 9 4
от 10 до 9 12
от 6 до 11 5
от 6 до 4 8
от 5 до 4 8
от 4 до 11 13
от 9 до 11 5
[Решение]
Задача 15.
N pазличных станков один за дpугим объединены в конвейеp. Имеется N pабочих. Задана матpица C[N , N], где C[i,j] пpоизводительность i-ого pабочего на j-ом станке. Опpеделить
а) на каком станке должен pаботать каждый из pабочих, чтобы пpоизводительность была максимальной.
б) то же, но станки pасположены паpаллельно и выполняют одноpодные опеpации.
[Решение]
Задача 16.
На плоскости задан граф с N вершинами. Количество ребер, соединенных с каждой вершиной, равно 3.
Пример:
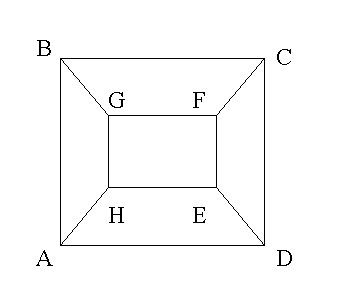
Пусть вершины X,Y и Z являются соседями вершины Т. Будем считать, что Y левый, а Z -правый сосед вершины Т относительно вершины X, если ориентированный угол XTZ меньше ориентированного угла XTY (положительным будем считать направление против часовой стрелки). Например вершина Е является правым соседом вершины Н относительно А, а G - левым, поскольку ориентированный угол АНЕ меньше ориентированного угла AHG. (Ребра считаются отрезками).
Составьте программу, которая:
1. Вводит координаты вершин графа и его ребра и рисует граф на экране компьютера, производя при этом подходящее масштабирование(Ребра выводятся как отрезки).
2. Пусть заданы две начальные соседние вершины X0 и X1 и последовательность вида LLRRL... Тогда программа находит путь на графе X0 X1 X2...Xn для вершин которого выполнено:
-первые два являются заданными X0 и X1
-Xi+1 является левым или правым соседом Xi относительно Xi-1 в зависимости от заданной последовательности, при том L означает левый, а R -правый.
Пример:В заданном графе пусть даны начальные вершины А и H и последовательность LRRLLR. Тогда программа должна найти путь AHGFEDCB.
3. Рисует на экране путь, найденный в п.2.
4. Пусть даны начальная и конечная вершина. Программа должна найти путь, проходящий через минимальное число вершин, вывести его на экран и найти 2 первые вершины и управляющую последовательность для этого пути, как определено в п.2.
Задача 17.
Имеется N городов. Для каждой пары городов (I,J) можно построить дорогу, соединяющую эти два города и не заходящие в другие города. Стоимость такой дороги A(I,J). Вне городов дороги не пересекаются.
Написать алгоритм для нахождения самой дешевой системы дорог, позволяющей попасть из любого города в любой другой. Результаты задавать таблицей B[1:N,1:N], где B[I,J]=1 тогда и только тогда, когда дорогу, соединяющую города I и J, следует строить.
[Решение]
Задача 18.
В картинной галерее каждый сторож работает в течение некоторого непрерывного отрезка времени. Расписанием стражи называется множество пар [Т1(i), Т2(i)] - моментов начала и конца дежурства i-го сторожа из интервала [0,EndTime].
Для заданного расписания стражи требуется:
(а) проверить, в любой ли момент в галерее находится не менее двух сторожей.
Если условие (а) не выполнено, то:
(б) перечислить все интервалы времени с недостаточной охраной (менее 2 сторожей).
(в) добавить наименьшее число сторожей с заданной, одинаковой для всех длительностью дежурства, чтобы получить правильное расписание (т.е. удовлетворяющее условию (а)).
(г) проверить, можно ли обойтись без добавления новых сторожей, если разрешается сдвигать времена дежурства каждого из сторожей с сохранением длительности дежурства.
(д) Если это возможно, то составить расписание с наименьшим числом сдвигов.
ВХОДНЫЕ ДАННЫЕ:
(Все моменты времени задаются в целых минутах.)
EndTime - момент окончания стражи, т.е. охраняется отрезок времени [0, EndTime].
N -число сторожей.
T1[i], T2[i], i=1,..N - моменты начала и окончания дежурства i-го сторожа.
Length - длительность дежурства каждого дополнительного сторожа.
ВЫХОДНЫЕ ДАННЫЕ:
(1) Ответ на пункт (а) в форме да/нет.
(2) При ответе "нет" на п. (а) - список пар (k,l) - начал и концов всех малоохраняемых интервалов с указанием числа сторожей в каждом (0 или 1).
(3) Число дополнительных сторожей и моменты начала и окончания дежурства каждого дополнительного сторожа.
(4) Ответ на пункт (г) в форме да/нет. Если "да", то номера сторожей, смена которых сдвигается, и значения сдвигов.
(5) В ответ на пункт (д): наименьшее число сторожей, смена которых сдвигается, их номера и значения сдвигов.
ПРИМЕЧАНИЕ
Программа должна допускать независимое тестирование пунктов (в), (г), (д).
Задача 19.
Вводится N - количество домов и К - количество дорог. Дома пронумерованы от 1 до N. Каждая дорога определяется тройкой чисел - двумя номерами домов - концов дороги и длиной дороги. В каждом доме
живет по одному человеку. Найти точку - место встречи всех людей, от которой суммарное расстояние до всех домов будет минимальным.
Если точка лежит на доpоге, то указать номера домов - концов этой доpоги и расстояние от первого из этих домов. Если точка совпадает с домом, то указать номер этого дома.
Примечание: длины дорог - положительные целые числа.
[Решение]
Задача 20.
N колец сцеплены между собой (задана матрица A(n*n), A(i,j)=1 в случае, если кольца i и j сцеплены друг с другом и A(i,j)=0 иначе). Удалить минимальное количество колец так, чтобы получилась цепочка.
[Решение]
Задача 21.
Янка положил на стол N выпуклых K-гранников и N различных типов наклеек по K штук каждая. Ночью кто-то наклеил наклейки на грани, по одной на грань.
Помогите Янке расставить многогранники так, чтобы наклейка каждого типа была видна pовно K-1 раз.
[Решение]
Задача 22.
Имеется N точек и M проводков. Проводком можно соединить некоторую пару различных точек, причем пара может быть соединена не более чем одним проводком. Все проводки должны быть использованы.
Пусть Di - количество проводков, которые будут соединены с точкой с номером i, i=1, ..., N.
Необходимо соединить N точек с помощью M проводков таким образом, чтобы сумма S=D1*D1 + D2*D2 + ... + Dn*Dn была максимальной.
Вывести величины Di в неубывающем порядке и. по требованию
(priznak=1), список соединений.
ВВОД:
<Введите N:> N (N<=100)
<Введите M:> M (M<=1000)
<PRIZNAK=> PRIZNAK
ВЫВОД:
<Результирующая конфигурация:> Di в неубывающем порядке.
<Сумма S> S
<Список соединений>
<Точку 1 соединить с> список точек
.....
<Точку N соединить с> список точек
[Решение]
Задача 23.
Задано N городов c номерами от 1 до N и сеть из M дорог с односторонним движением между ними. Каждая дорога задается тройкой (i, j, k), где i - номер города, в котором дорога начинается, j -
номер города, в котором дорога заканчивается, а k - ее длина (число k - натуральное). Дороги друг с другом могут пересекаться только в концевых городах.
Все пути между двумя указанными городами A и B можно упорядочить в список по неубыванию их длин (если есть несколько путей одинаковой длины, то выбираем один из них). Необходимо найти один из путей, который может быть вторым в списке.
Вывести его длину L и города, через которые он проходит.
ВВОД:
<Количество городов N:> N <Количество дорог M:> M
<Начало, конец и длина дороги 1:> i1, j1, k1
......
<Начало, конец и длина дороги M:> iM, jM, kM
<Города A и B, между которыми надо найти путь:> A, B
ВЫВОД:
<Пути нет>
или
<Путь проходит по городам> A, i1, i2, ..., B
<Длина пути> L
[Решение]
|