
|
Метод выделения lcs для двух входных строк x и y Ханта и Шиманского (Hunt, Szymanski) эквивалентен нахождению максимального монотонно возрастающего пути в графе, состоящего из точек (i, j), таких, что xi = yj. Мы опишем этот метод, а затем проиллюстрируем его примером.
Для удобства будем считать, что длины входных строк равны, то есть |x| = |y| = n. Алгоритм легко изменить так, чтобы он подходил и для строк разной длины. Количество упорядоченных пар позиций совпадающих символов x и y, то есть мощность множества {(i,j) : xi = yj}, обозначим r.
Ключевым в методе является массив значений ki,l, определяемых соотношением
|
ki,s = min j, для которых li,j = s
|
(30) |
где li,j определены в (14).
Таким образом, значение ki,l дает длину самого короткого префикса y, имеющего общую с префиксом x длины i общую подпоследовательность длины s. Вот пример: если x = preterit и y = zeitgeist, то k5,1 = 2, k5,2 = 4, k5,3 = 6, а k5,4 и k5,5 не определены.
Из того, что ki,s по определению является минимальным значением, следует, что последний символ подпоследовательности длины s, общей для префиксов x(1, i) и y(1, ki,j) равен 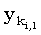 . Итак, длина lcs для x(1, i) и y(1, ki,s-1) равна s - 1. Следовательно, ki,s-1 < ki,s-1, то есть ki,s-1 < ki,s. Отсюда видно, что значения ki,s в каждой строке массива должны монотонно возрастать. . Итак, длина lcs для x(1, i) и y(1, ki,s-1) равна s - 1. Следовательно, ki,s-1 < ki,s-1, то есть ki,s-1 < ki,s. Отсюда видно, что значения ki,s в каждой строке массива должны монотонно возрастать.
Значения k можно итеративно вычислять по предыдущим значениям в массиве. В частности, значение ki+1,s может быть выведено по ki,s-1 и ki,s. Перед тем, как продемонстрировать, как это делается, исследуем диапазон значений, в который должно попасть ki+1,s.
Общая для x(1, i) и y(1, ki,s) подпоследовательность длины s будет общей и для x(1, i+1) и y(1, ki,s). Таким образом,
По определению, x(1, i+1) и y(1, ki+1,s) имеют lcs длины s. Поэтому lcs, построенная для префиксов на один символ более коротких, а именно x(1,i) и y(1, ki+1,s-1), будет короче ее не больше, чем на один символ. Таким образом,
Комбинируя (31) и (32), получаем следующие границы для ki+1,s
|
ki,s-1 < ki+1,s < ki,s
|
(33) |
Правило вычисления ki+1,s по ki,s-1 и ki,s выглядит так:
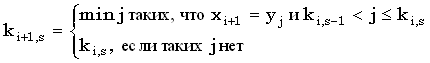
|
(34) |
Правильность этого выражения можно доказать следующим образом. Сначала рассмотрим случай, когда подходящих j не существует. Так как ki+1,s является минимальным значением, последняя компонента любой общей для x(1, i+1) и y(1, ki+1,s) подпоследовательности длины s должна быть равна 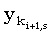 . Из того, что ki+1,s должно лежать внутри задаваемых (33) границ, следует, что . Из того, что ki+1,s должно лежать внутри задаваемых (33) границ, следует, что 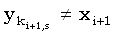 , иначе требуемым значением j было бы ki+1,s. Отсюда, в свою очередь, следует, что эта подпоследовательность длины s является общей для x(1,i) и y(1,ki+1,s), откуда ki,s < ki+1,s. Комбинируя это с (33) получаем, что когда подходящих j не существует, ki+1,s = ki,s. , иначе требуемым значением j было бы ki+1,s. Отсюда, в свою очередь, следует, что эта подпоследовательность длины s является общей для x(1,i) и y(1,ki+1,s), откуда ki,s < ki+1,s. Комбинируя это с (33) получаем, что когда подходящих j не существует, ki+1,s = ki,s.
Теперь рассмотрим случай, когда существует j, при котором xi+1 = yj и ki,s-1 < j < ki,s. Префиксы x(1, i+1) и y(1, j) будут иметь общую подпоследовательность длины s, равную подпоследовательности длины s-1, общей для x(1,i) и y(1, ki,s-1) с присоединенным на конце символом xi+1 (так как xi+1 = yj). Таким образом, ki+1,s < j. Теперь осталось узнать, достигнуто ли желаемое равенство, или ki+1,s на самом деле меньше нашего значения j. Предположив последнее, и придя к противоречию, мы тем самым докажем, что выполняется первое. Итак, предположим, что ki+1,s < j. И снова, последним символом общей для x(1, i+1) и y(1, ki+1,s) последовательности длины s должен быть yk+1,s. Так как ki+1,j и j должны лежать в одном интервале (из (33) и (34)), мы знаем, что yk+1,s =/=xi+1, поскольку j является минимальным значением в разрешенном диапазоне, при котором yj = xi+1, а мы предполагаем, что ki+1,s < j. Отсюда следует, что x(1,i) и y(1, ki+1,s) также имеют общую подпоследовательность длины s, поэтому ki,s < ki+1,s. Вместе с (33) это означает, что ki,s = ki+1,s. Мы предположили, что ki+1,s < j. Таким образом, из (34), ki+1,s < ki,s, что противоречит предыдущему результату. Это показывает, что на самом деле j равно требуемому ki+1,s.
Алгоритм для определения |lcs(x,y)| с помощью ki,s дан на рисунке 15. Вектор kk используется как i-я строка массива k. Таким образом, в начале i-й итерации kks = ki-1,s для 0 < s < n, а по завершению итерации, kks = ki,s при 0 < s < n. Обратите внимание, что kk0 присваивается значение 0, а остальным kk – значение n+1, обозначая неопределенные значения ki,s. Для вычислений требуется только одна строка, так как значения столбцом ниже остаются неизменными или уменьшаются, а значения вдоль строки остаются монотонно возрастающими.
- инициализация
kk0 = 0
for s = 1 to n
kks = n + 1
- вычисление |lcs(x,y)|
for i = 1 to n
for j = n downto 1
if xi = yi
найти s, для которого kks-1 < J < kks
kks = j
print max s такое, что kks =/=n + 1
Рис. 15: Вычисление |lcs(x,y)| по Ханту-Шиманскому
Важно, что в цикле по j идет уменьшение индекса с n до 1. Рассмотрим случай, когда xi совпадает с несколькими символами в y, скажем, 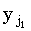 , , 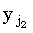 , ... , , ... , , такими, что ki-1,s-1 < j1 < j2 < ... <jp < ki-1,s. Из (34) можно видеть, что правильным значением ki,s является j1. В процессе итераций, с уменьшением индекса j, ki,s будут присваиваться все меньшие значения jp, jp-1, …, j1, пока в конце не будет присвоено требуемое значение. Если, итерации по j проводить в противоположном направлении, то ki,s сначала будет присвоено правильное значение, однако затем ki,s+1 будет установлено равным j2, ki,s+2 равным j3, и так до ki,s+p-1, что правильным не является. , такими, что ki-1,s-1 < j1 < j2 < ... <jp < ki-1,s. Из (34) можно видеть, что правильным значением ki,s является j1. В процессе итераций, с уменьшением индекса j, ki,s будут присваиваться все меньшие значения jp, jp-1, …, j1, пока в конце не будет присвоено требуемое значение. Если, итерации по j проводить в противоположном направлении, то ki,s сначала будет присвоено правильное значение, однако затем ki,s+1 будет установлено равным j2, ki,s+2 равным j3, и так до ki,s+p-1, что правильным не является.
В конце процедуры значение |lcs(x,y)| задается максимальным s, для которого определено kn,s. Так как значения kk монотонно возрастают, операция ‘найти’ может быть реализована за время O(log n) путем бинарного поиска. Из того, что инструкция if выполняется ровно n2, следует, что алгоритм выполняется за время O(n2 log n) в худшем случае. Заметим, что в случае строк разной длины граница для инициализации kk и внешнего цикла i будет равна m, а не n, где m < n. Ниже приведены результаты процедуры, где показаны значения ki,s для x = preterit и y = zeitgeist. Из последней строки можно видеть, что |lcs(preterit, zeitgeist)| = 5.
|
i |
s |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
p |
0 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
|
2 |
r |
0 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
|
3 |
e |
0 |
2 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
|
4 |
t |
0 |
2 |
4 |
10 |
10 |
10 |
10 |
10 |
10 |
|
5 |
e |
0 |
2 |
4 |
6 |
10 |
10 |
10 |
10 |
10 |
|
6 |
r |
0 |
2 |
4 |
6 |
10 |
10 |
10 |
10 |
10 |
|
7 |
i |
0 |
2 |
3 |
6 |
7 |
10 |
10 |
10 |
10 |
|
8 |
t |
0 |
2 |
3 |
4 |
7 |
9 |
10 |
10 |
10 |
Исчерпывающий поиск совпадающих символов в приведенном выше алгоритме довольно неэффективен, и его можно избежать, предварительно обработав строки, чтобы получить предварительную запись позиций, в которых они совпадают. Таким образом, можно построить массив указателей matchlist на связанные списки, в котором matchlist[i] дает связанный список позиций j, в которых xi = yj, идущих в порядке убывания. Для повторяющихся экземпляров символа в x можно использовать один и тот же список. Например, списки для x = preterit и y = zeitgeist будут следующими.
matchlist[1] = ()
matchlist[2] = ()
matchlist[3] = (6, 2)
matchlist[4] = (9, 4)
matchlist[5] = matchlist[3]
matchlist[6] = ()
matchlist[7] = (7, 3)
matchlist[8] = matchlist[4]
Окончательный алгоритм, включающий это улучшение, а также извлекающий lcs двух строк, представлен на рисунке 16. lcs воссоздается с помощью средства поиска с возвратами, используемого при вычислении значений kk. Когда определяется kkj, links устанавливается указывающим на оглавление списка пар (i, j), определяющий общую подпоследовательность длины s. Это реализуется процедурой newnode, создающей узел, содержащий текущую пару (i, j) с указателем на предыдущий узел в списке и возвращающей указатель на только что созданный узел.
создать списки с использованием указателей
for i = 1 to n
matchlist[i] = (j1, j2, . . . , jp) такие, что
j1 > j2 > … >jp и 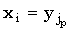 для 1 < q < p
- инициализация
kk0 = 0
for s = 1 to n
kkl = n + 1
link0 = null
- вычисление последовательных значений kk
for i = 1 to n
for j in matchlist[i]
найти s такое, что kks-1 < J < kks
if j < KKs
kks = j
links = newnode(i, j, links-1)
- выделение lcs в обратном порядке
s = max s такое, что kks =/=n + 1
pointer = links
while pointer =/=null
print (i,j) пара указана с помощью pointer
продвинуть pointer для 1 < q < p
- инициализация
kk0 = 0
for s = 1 to n
kkl = n + 1
link0 = null
- вычисление последовательных значений kk
for i = 1 to n
for j in matchlist[i]
найти s такое, что kks-1 < J < kks
if j < KKs
kks = j
links = newnode(i, j, links-1)
- выделение lcs в обратном порядке
s = max s такое, что kks =/=n + 1
pointer = links
while pointer =/=null
print (i,j) пара указана с помощью pointer
продвинуть pointer
Рисунок 16: Вычисление lcs(x,y) по Ханту-Шиманскому
Предварительную обработку можно реализовать, сортируя символы каждой строки, записывая их исходные позиции, и сливая затем отсортированные строки для создания списков matchlist. С помощью алгоритма пирамидальной сортировки (heapsort) эту фазу можно выполнить за время O(n log n) с использованием O(n) памяти. Стадия инициализации занимает время O(n). Во время вычисления значений kk внутренний цикл выполняется r раз. Для каждой итерации выполняется бинарный поиск и несколько других операций с фиксированным временем. Таким образом, эта стадия занимает время O(r+r * log n) и включает создание r новых узлов. Наконец, фактическое выделение lcs занимает время O(|lcs(x,y)|), которое, разумеется, равно O(n). Таким образом, общие затраты времени и памяти у алгоритмы равны, соответственно, O((r+n) * log n) и O(r+n). И снова, более общий случай строк неравной длины легко реализуется установкой границ для инициализации kk и циклов i равными m вместо n.
В примере вычисления lcs(preterit, zeitgeist) описанная выше процедура выдает следующий список пар (i, j) для lcs (в обратном порядке):
(8, 9), (7, 7), (5, 6), (4, 4), (3, 2).
Это проиллюстрировано ниже, где узлы указывают точки (i, j), такие что xi = xj. lcs формируется символами в соответствии с заполненными узлами, а именно eteit, и, таким образом, эквивалентна максимальному монотонно возрастающему пути в графе.
|
|
j |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
i |
|
z |
e |
i |
t |
g |
e |
i |
s |
t |
|
1 |
p |
|
|
|
|
|
|
|
|
|
|
2 |
r |
|
|
|
|
|
|
|
|
|
|
3 |
e |
|
 |
|
|
|
 |
|
|
|
|
4 |
t |
|
|
|
 |
|
|
|
|
 |
|
5 |
e |
|
 |
|
|
|
 |
|
|
|
|
6 |
r |
|
|
|
|
|
|
|
|
|
|
7 |
i |
|
|
 |
|
|
|
 |
|
|
|
8 |
t |
|
|
|
 |
|
|
|
|
 |
Апостолико и Гиерра [Apostolico, Guerra, 1987] разработали версию алгоритма Ханта-Шиманского, в которой удалось избежать снижения эффективности последнего до уровня ниже квадратичной в худшем случае. Вариант Апостолико и Гиерра имеет временную сложность O(m * log n + t * log(2mn/t)), что в худшем случае равно O(mn). Здесь t < r равняется числу доминантных совпадений между строками. k-доминантное совпадение является упорядоченной парой (i, j), такой, что xi = yj, li,j = k, и это первое появление такой точки в подматрице l(1,...,i),(1,...,j) (li,j определяется в (14)). Сопоставление (i, j), таким образом, является доминантным, если вхождение в подходящей строке префиксов каждой lcs(x(1,i),y(1,j)) заканчивается символами xi и yj. Вариант Апостолико и Гиерра имеет эффективные средства нахождения доминантных сопоставлений и включает структуры данных, называемые характеристическими деревьями, для представления различных списков, требуемых алгоритмом.
Верхнюю границу (Джекобсон и Во [Jacobson, Vo, 1992]) для общего числа доминантных совпадений t между двумя строками получают следующим образом. k-доминантные совпадения можно отсортировать в порядке возрастания i, чтобы получить 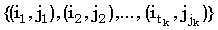 , где tk есть число k-доминантных совпадений, и , где tk есть число k-доминантных совпадений, и 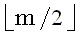 . Так как индексы i и j монотонно убывают и возрастают, соответственно, мы имеем следующие неравенства, где i < p < tk: . Так как индексы i и j монотонно убывают и возрастают, соответственно, мы имеем следующие неравенства, где i < p < tk:
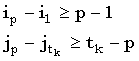
|
(35) |
Расстояние редактирования между префиксами x(1, i) и y(1, j) и длина их lcs связаны между собой следующим соотношением:
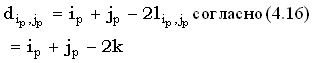
|
(36) |
Так как сопоставление (i1, j1) является k-доминантным, мы имеем i1 > k, а также, раз 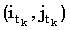 является k-доминантным, является k-доминантным, 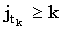 . Объединяя это с (36), получаем: . Объединяя это с (36), получаем:
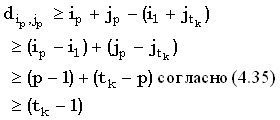
|
(37) |
Пусть k'обозначает число, при котором имеется больше всего k-доминантных совпадений. lcs(x,y), построенная только по доминантным совпадениям, должна содержать одно из этих k'-доминантных совпадений, скажем, (ip, jp). Расстояние между полными строками x и y не может быть меньше расстояния между префиксами x(1, i) и y(1, j), то есть:
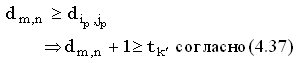
|
(38) |
Так как 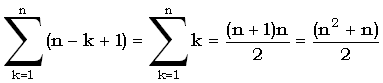 является максимальным числом доминантных совпадений, то есть является максимальным числом доминантных совпадений, то есть 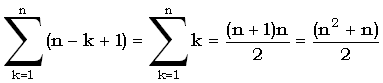 > tl при 1 < l < lm,n, имеем: > tl при 1 < l < lm,n, имеем:
|
t < lm,n 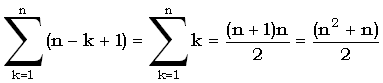
|
(39) |
Комбинируя это с неравенством (38), получаем окончательный результат для верхней границы общего числа доминантных совпадений:
Число доминантных совпадений может быть гораздо меньше общего числа совпадений, особенно когда расстояние между строками мало. Граница для t в худшем случае выводится следующим образом. Подставляя вместо dm,n выражение (16), получаем следующее:
|
t < lm,n (m + n - 2lm,n + 1)
|
(41) |
Для строк равной длины, эта граница достигает максимального значения, равного (2n+1)2/8, при длине lcs, равной (2n+1)/4. Вспомним, что максимальное число совпадений равно n2. Таким образом, можно видеть, что общее число совпадений асимптотически превышает число доминантных совпадений вдвое.
|