
|
При рассмотрении массива расстояний из метода Вагнера-Фишера становится очевидно, что при таком подходе требования к памяти равны O(mn). Чтобы избежать проблем с памятью при работе с длинными строками, Хиршберг разработал линейную относительно затрат памяти версию этого алгоритма.
Цель Хиршберга состояла в том, чтобы найти lcs(x,y) для строк x и y. Поэтому вместо расстояний между строками определялись длины самых длинных общих подпоследовательностей у все более и более длинных префиксов. Обозначим их как li,j, то есть:
|
li,j = |lcs(x(1,i), y(1,j))|
|
(14) |
Для данной метрики существует фиксированная взаимосвязь между li,j и di,j. Рассмотрим, например, расстояние редактирование, определяемое следующим ценовыми весами.
w(a,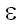 ) = 1 ) = 1
|
(15) |
w(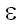 ,b) = 2, если a =/=b и 0 в противном случае ,b) = 2, если a =/=b и 0 в противном случае
|
Из следа минимальной цены из x в y можно видеть, что расстояние редактирования d(x, y) связано с |lcs(x,y)| выведенным ниже соотношением, где del, ins и sub являются, соответственно, количествами удалений, вставок и замен символов.
d(x,y) = del + ins + 2sub
= m - (|lcs(x,y)| + sub) + n - (|lcs(x,y)| + sub) + 2sub
= m + n - 2 |lcs(x,y)|
|
(16)
|
Отсюда получаем взаимосвязь между li,j и di,j:
|
li,j = (i + j - di,j)/2
|
(17) |
С помощью этого преобразования процедуру динамического программирования для li,j можно вывести из аналогичной процедуры для di,j, см. рисунок 12. Так как длина lcs любой строки и пустой равна 0, значения границ массива задаются как li,0 = l0,j = 0. Как и в случае с di,j, значения li,j строятся по предыдущим результатам. В позиции (i,j), то есть когда рассматриваются префиксы x(1,i) и y(1,j), если xi = yj, мы получаем новую lcs, присоединяя этот символ к текущей lcs префиксов x(1, i - 1) и y(1, j - 1), откуда li,j = li-1,j-1 +1. Иначе длина текущей lcs просто равна максимальному из предыдущих соседних значений.
- инициализация границ массива
l0,0 = 0
for i = 1 to m
li,0 = 0
for j = 1 to n
l0,j = 0
- вычисление li,j
for i = 1 to m
for j = 1 to n
if xi = yj
li,j = li-1,j-1 + 1
else
li,j = max{li-1,j, li,j-1}
Рисунок 12: Вычисление |lcs(x,y)|
Затраты памяти можно сократить, если обратить внимание, что для вычисления строки i требуется только строка i-1. Это соображение используется в алгоритме, приведенном на рисунке 13. Он выдает вектор ll, где llj = lm,j. Используется массив h длины 2(n+1), в котором строки 0 и 1 выступают в качестве строк i-1 и i массива l, соответственно. Поэтому перед вычислением каждой новой ‘строки i’ строка 1 сдвигается вверх на место строки 0.
lcs_lengh(m, n, x, y, ll)
- инициализация
for j = 0 to n
h1,j = 0
- вычисление h1,j
for i = 1 to m
- сдвиг строки вверх
for j = 0 to n
h0,j = h1,j
for j = 1 to n
if xi = yj
h1,j = h0,1 + 1
else
h1,j = max{h1,j-1, h0,j}
- копирование результата в выходной вектор
for j = 0 to n
llj = h1,j
Рисунок 13: Вычисление |lcs(x,y)| с сокращенными затратами памяти
Как и раньше, инструкция if исполняется ровно mn раз, что дает временную сложность O(mn). Входной и выходной массивы требуют m+n+(n+1) ячеек, плюс 2(n+1) ячеек, выделенных для массива h. Поэтому пространственная сложность является линейной по m и n, то есть O(m+n). Этот метод можно использовать для определения lcs(x,y) с линейными затратами памяти, как описано ниже.
Основная идея состоит в том, чтобы рекурсивно делить строку x пополам, и для каждой половины, x1 и x2, находить соответствующие префикс и суффикс, y1 и y2 строки y, такие, что lcs для x1 и y1, соединенные с lcs для x2 и y2, равны lcs полных строк x и y, то есть:
lcs(x1,y1) lcs(x2,y2) = lcs(x,y) lcs(x2,y2) = lcs(x,y)
|
(18) |
Таким образом, задачу можно рекурсивно разбивать на подзадачи, до сведения их к тривиальным.
Обозначим длину lcs суффиксов x(i+1, m) и y(j+1, n) как 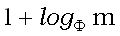 , то есть , то есть
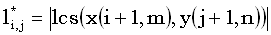
|
(19) |
Для 0 < j < n значения li,j являются длинами lcs префикса x(1, i) и различных префиксов y. Аналогично, для 0 < j < n значения 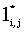 являются длинами lcs обращенного суффикса xR(m, i + 1) и различных префиксов обращенной строки yR. Следующая теорема позволяет находить подходящий префикс и суффикс y, когда x разделена пополам, то есть когда i берется равным являются длинами lcs обращенного суффикса xR(m, i + 1) и различных префиксов обращенной строки yR. Следующая теорема позволяет находить подходящий префикс и суффикс y, когда x разделена пополам, то есть когда i берется равным 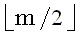 . Теорема гласит, что если x произвольным образом разделить на две части, то максимальное по всем разбиениям y надвое значение суммы длин lcs первых и вторых частей x и y равно длине lcs полных строк x и y. . Теорема гласит, что если x произвольным образом разделить на две части, то максимальное по всем разбиениям y надвое значение суммы длин lcs первых и вторых частей x и y равно длине lcs полных строк x и y.
Теорема
Определим Mi формулой
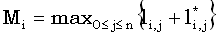
|
(20) |
Тогда
|
Mi = lm,n для 0 < i < m
|
(21) |
Доказательство
Пусть
 для j = j0 для j = j0
|
(22) |
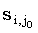 - произвольная lcs(x(1, i), y(1,j0)) - произвольная lcs(x(1, i), y(1,j0))
|
(23) |
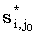 - произвольная lcs(x(i + 1, m), y(j0 + 1, n)) - произвольная lcs(x(i + 1, m), y(j0 + 1, n))
|
(24) |
тогда 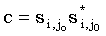 является общей подпоследовательностью x и y, и ее длина равна M. Таким образом, является общей подпоследовательностью x и y, и ее длина равна M. Таким образом,
lm,n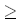 Mi Mi
|
(25) |
Пусть sm,n – произвольная lcs(x,y), тогда sm,n является подпоследовательностью y, равной s1 s2, где s1 – это подпоследовательность x(1,i), а s2 – подпоследовательность x(i+1,m). Таким образом, существует значение j1, такое, что s2 является подпоследовательностью y(1, j1), а s2 – подпоследовательностью y(j1+1, n). Длины s1 и s2 удовлетворяют следующим условиям: s2, где s1 – это подпоследовательность x(1,i), а s2 – подпоследовательность x(i+1,m). Таким образом, существует значение j1, такое, что s2 является подпоследовательностью y(1, j1), а s2 – подпоследовательностью y(j1+1, n). Длины s1 и s2 удовлетворяют следующим условиям:
|s1| < |lcs(x(1, i), y(1, j1))|
< 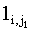 согласно (14) согласно (14)
|
(26) |
|
|s2| < |lcs(x(i + 1, m), y(j1 + 1, n))|
< 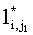 согласно (19) согласно (19)
|
(27) |
Таким образом,
lm,n = |sm,n|
= |s1| + |s2|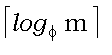 согласно (26) и (27) согласно (26) и (27)
< Mi согласно (20)
|
(28)
|
Из неравенств (25) и (28) получаем
что, собственно, и требовалось.
На рисунке 14 дан полный алгоритм определения lcs(x,y), использующий приведенную выше теорему. В результате возвращается строка c, равная lcs входных строк x и y. Для тривиальной задачи процедура возвращает пустую строку или односимвольную lcs. В противном случае строка x делится пополам, после чего ищутся длина lcs ее первой половины и префиксов y различной длины, и длина lcs ее второй половины и суффиксов y различной длины. Затем по теореме ищется первая позиция в y, обозначаемая здесь k, такая, что lcs первой половины x и y(1,k) в соединении с lcs второй половины x и y(k+1, n) равна требуемой lcs(x, y). Таким образом, остается только использовать это k в двух рекурсивных вызовах процедуры, чтобы получить требуемые lcs подзадач, и соединить их.
lcs(m, n, x, y, c)
- тривиальный случай
if n = 0
c = e
else if m = 1
if 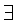 j, 0 < j < n, такое что x1 = y1
c = x1
else
c = e
- нетривиальный случай, разбиение задачи
else
i = [m/n]
-вычисление li,j и l*i,j для 0 < j < n
lcs_length(i, n, x(1,i), y(1,n), l1)
lcs_length(m-i, n, xR(m, i+1), yR(n,1), l2)
найти j, такое, что li,j + l*i,j = lm,n
M = max {l1j + l2n-j : 0 < j < n}
k = min j таких, что l1j + l2n-j = M
- решение более простой задачи
lcs(i, k, x(1, i), y(1, k), c1)
lcs(m - i, n - k, x(i + 1, m), y(k + 1, n), c2)
- конкатенация результатов - окончательный результат
c = c1 j, 0 < j < n, такое что x1 = y1
c = x1
else
c = e
- нетривиальный случай, разбиение задачи
else
i = [m/n]
-вычисление li,j и l*i,j для 0 < j < n
lcs_length(i, n, x(1,i), y(1,n), l1)
lcs_length(m-i, n, xR(m, i+1), yR(n,1), l2)
найти j, такое, что li,j + l*i,j = lm,n
M = max {l1j + l2n-j : 0 < j < n}
k = min j таких, что l1j + l2n-j = M
- решение более простой задачи
lcs(i, k, x(1, i), y(1, k), c1)
lcs(m - i, n - k, x(i + 1, m), y(k + 1, n), c2)
- конкатенация результатов - окончательный результат
c = c1 c2 c2
Рисунок 14: Вычисление lcs(x,y) по Хиршбергу
В линейности этого алгоритма можно убедиться следующим образом. Строки x и y можно держать в глобальном хранилище, а параметры подстроки можно передавать как указатели аргументов начала и конца подходящих подстрок. Как было показано, вызовы lcs_length требуют временного хранилища, пропорционального m и n. Не считая рекурсивных вызовов, требования к памяти в процедуре lcs являются постоянными. Можно показать, что всего производится 2m - 1 вызовов lcs. Таким образом, общие требования линейны по m и n, то есть затраты памяти у этого метода определения lcs составляют O(m + n). Хиршберг [Hirschberg, 1975] проанализировал также временные затраты этого алгоритма, и показал, что они равны O(mn).
|