Проблемы алгоритмов архивации с потерями

Первыми для архивации изображений стали применяться привычные алгоритмы. Те, что использовались и используются в системах резервного копирования, при создании дистрибутивов и т.п. Эти алгоритмы архивировали информацию без изменений. Однако основной тенденцией в последнее время стало использование новых классов изображений. Старые алгоритмы перестали удовлетворять требованиям, предъявляемым к архивации. Многие изображения практически не сжимались, хотя “на взгляд” обладали явной избыточностью. Это привело к созданию нового типа алгоритмов — сжимающих с потерей информации. Как правило, коэффициент архивации и, следовательно, степень потерь качества в них можно задавать. При этом достигается компромисс между размером и качеством изображений.

Одна из серьезных проблем машинной графики заключается в том, что до сих пор не найден адекватный критерий оценки потерь качества изображения. А теряется оно постоянно — при оцифровке, при переводе в ограниченную палитру цветов, при переводе в другую систему цветопредставления для печати, и, что для нас особенно важно, при архивации с потерями. Можно привести пример простого критерия: среднеквадратичное отклонение значений пикселов (L₂ мера, или root mean square — RMS):

По нему изображение будет сильно испорчено при понижении яркости всего на 5% (глаз этого не заметит — у разных мониторов настройка яркости варьируется гораздо сильнее). В то же время изображения со “снегом” — резким изменением цвета отдельных точек, слабыми полосами или “муаром” будут признаны “почти не изменившимися” (Объясните, почему?). Свои неприятные стороны есть и у других критериев.

Рассмотрим, например, максимальное отклонение:

Эта мера, как можно догадаться, крайне чувствительна к биению отдельных пикселов. Т.е. во всем изображении может существенно измениться только значение одного пиксела (что практически незаметно для глаза), однако согласно этой мере изображение будет сильно испорчено.

Мера, которую сейчас используют на практике, называется мерой отношения сигнала к шуму (peak-to-peak signal-to-noise ratio — PSNR).

Данная мера, по сути, аналогична среднеквадратичному отклонению, однако пользоваться ей несколько удобнее за счет логарифмического масштаба шкалы. Ей присущи те же недостатки, что и среднеквадратичному отклонению.

Лучше всего потери качества изображений оценивают наши глаза. Отличной считается архивация, при которой невозможно на глаз различить первоначальное и разархивированное изображения. Хорошей — когда сказать, какое из изображений подвергалось архивации, можно только сравнивая две находящихся рядом картинки. При дальнейшем увеличении степени сжатия, как правило, становятся заметны побочные эффекты, характерные для данного алгоритма. На практике, даже при отличном сохранении качества, в изображение могут быть внесены регулярные специфические изменения. Поэтому алгоритмы архивации с потерями не рекомендуется использовать при сжатии изображений, которые в дальнейшем собираются либо печатать с высоким качеством, либо обрабатывать программами распознавания образов. Неприятные эффекты с такими изображениями, как мы уже говорили, могут возникнуть даже при простом масштабировании изображения.
 

JPEG — один из самых новых и достаточно мощных алгоритмов. Практически он является стандартом де-факто для полноцветных изображений [1]. Оперирует алгоритм областями 8х8, на которых яркость и цвет меняются сравнительно плавно. Вследствие этого, при разложении матрицы такой области в двойной ряд по косинусам (см. формулы ниже) значимыми оказываются только первые коэффициенты. Таким образом, сжатие в JPEG осуществляется за счет плавности изменения цветов в изображении.

Алгоритм разработан группой экспертов в области фотографии специально для сжатия 24-битных изображений. JPEG — Joint Photographic Expert Group — подразделение в рамках ISO — Международной организации по стандартизации. Название алгоритма читается ['jei'peg]. В целом алгоритм основан на дискретном косинусоидальном преобразовании (в дальнейшем ДКП), применяемом к матрице изображения для получения некоторой новой матрицы коэффициентов. Для получения исходного изображения применяется обратное преобразование.

ДКП раскладывает изображение по амплитудам некоторых частот. Таким образом, при преобразовании мы получаем матрицу, в которой многие коэффициенты либо близки, либо равны нулю. Кроме того, благодаря несовершенству человеческого зрения, можно аппроксимировать коэффициенты более грубо без заметной потери качества изображения.

Для этого используется квантование коэффициентов (quantization). В самом простом случае — это арифметический побитовый сдвиг вправо. При этом преобразовании теряется часть информации, но могут достигаться большие коэффициенты сжатия.

Как работает алгоритм

Итак, рассмотрим алгоритм подробнее. Пусть мы сжимаем 24-битное изображение.

Шаг 1.

Переводим изображение из цветового пространства RGB, с компонентами, отвечающими за красную (Red), зеленую (Green) и синюю (Blue) составляющие цвета точки, в цветовое пространство YCrCb (иногда называют YUV).

В нем Y — яркостная составляющая, а Cr, Cb — компоненты, отвечающие за цвет (хроматический красный и хроматический синий). За счет того, что человеческий глаз менее чувствителен к цвету, чем к яркости, появляется возможность архивировать массивы для Cr и Cb компонент с большими потерями и, соответственно, большими коэффициентами сжатия. Подобное преобразование уже давно используется в телевидении. На сигналы, отвечающие за цвет, там выделяется более узкая полоса частот.

Упрощенно перевод из цветового пространства RGB в цветовое пространство YCrCb можно представить с помощью матрицы перехода:

Обратное преобразование осуществляется умножением вектора YUV на обратную матрицу.

Шаг 2.

Разбиваем исходное изображение на матрицы 8х8. Формируем из каждой три рабочие матрицы ДКП — по 8 бит отдельно для каждой компоненты. При больших коэффициентах сжатия этот шаг может выполняться чуть сложнее. Изображение делится по компоненте Y — как и в первом случае, а для компонент Cr и Cb матрицы набираются через строчку и через столбец. Т.е. из исходной матрицы размером 16x16 получается только одна рабочая матрица ДКП. При этом, как нетрудно заметить, мы теряем 3/4 полезной информации о цветовых составляющих изображения и получаем сразу сжатие в два раза. Мы можем поступать так благодаря работе в пространстве YCrCb. На результирующем RGB изображении, как показала практика, это сказывается несильно.

Шаг 3.

Применяем ДКП к каждой рабочей матрице. При этом мы получаем матрицу, в которой коэффициенты в левом верхнем углу соответствуют низкочастотной составляющей изображения, а в правом нижнем — высокочастотной.

В упрощенном виде это преобразование можно представить так:

Шаг 4.

Производим квантование. В принципе, это просто деление рабочей матрицы на матрицу квантования поэлементно. Для каждой компоненты (Y, U и V), в общем случае, задается своя матрица квантования q[u,v] (далее МК).

В стандарт JPEG включены рекомендованные МК, построенные опытным путем. Матрицы для большего или меньшего коэффициентов сжатия получают путем умножения исходной матрицы на некоторое число gamma.

С квантованием связаны и специфические эффекты алгоритма. При больших значениях коэффициента gamma потери в низких частотах могут быть настолько велики, что изображение распадется на квадраты 8х8. Потери в высоких частотах могут проявиться в так называемом “эффекте Гиббса”, когда вокруг контуров с резким переходом цвета образуется своеобразный “нимб”.

Шаг 5.

Переводим матрицу 8x8 в 64-элементный вектор при помощи “зигзаг”-сканирования, т.е. берем элементы с индексами (0,0), (0,1), (1,0), (2,0)...

Таким образом, в начале вектора мы получаем коэффициенты матрицы, соответствующие низким частотам, а в конце — высоким.

Шаг 6.

Свертываем вектор с помощью алгоритма группового кодирования. При этом получаем пары типа (пропустить, число), где “пропустить” является счетчиком пропускаемых нулей, а “число” — значение, которое необходимо поставить в следующую ячейку. Так, вектор 42 3 0 0 0 -2 0 0 0 0 1 ... будет свернут в пары (0,42) (0,3) (3,-2) (4,1) ... .

Шаг 7.

Свертываем получившиеся пары кодированием по Хаффману с фиксированной таблицей.

Процесс восстановления изображения в этом алгоритме полностью симметричен. Метод позволяет сжимать некоторые изображения в 10-15 раз без серьезных потерь.

Существенными положительными сторонами алгоритма является то, что:

1. Задается степень сжатия.
2. Выходное цветное изображение может иметь 24 бита на точку.

1. При повышении степени сжатия изображение распадается на отдельные квадраты (8x8). Это связано с тем, что происходят большие потери в низких частотах при квантовании, и восстановить исходные данные становится невозможно.
2. Проявляется эффект Гиббса — ореолы по границам резких переходов цветов.

Последнее требование сделало возможным появление таких игрушек, как цифровые фотоаппараты — устройства, размером с небольшую видеокамеру, снимающие 24-битовые фотографии на 10-20 Мб флэш карту с интерфейсом PCMCIA. Потом эта карта вставляется в разъем на вашем лэптопе и соответствующая программа позволяет считать изображения. Не правда ли, если бы алгоритм был несимметричен, было бы неприятно долго ждать, пока аппарат “перезарядится” — сожмет изображение.

Не очень приятным свойством JPEG является также то, что нередко горизонтальные и вертикальные полосы на дисплее абсолютно не видны и могут проявиться только при печати в виде муарового узора. Он возникает при наложении наклонного растра печати на горизонтальные и вертикальные полосы изображения. Из-за этих сюрпризов JPEG не рекомендуется активно использовать в полиграфии, задавая высокие коэффициенты. Однако при архивации изображений, предназначенных для просмотра человеком, он на данный момент незаменим.

Широкое применение JPEG долгое время сдерживалось, пожалуй, лишь тем, что он оперирует 24-битными изображениями. Поэтому для того, чтобы с приемлемым качеством посмотреть картинку на обычном мониторе в 256-цветной палитре, требовалось применение соответствующих алгоритмов и, следовательно, определенное время. В приложениях, ориентированных на придирчивого пользователя, таких, например, как игры, подобные задержки неприемлемы. Кроме того, если имеющиеся у вас изображения, допустим, в 8-битном формате GIF перевести в 24-битный JPEG, а потом обратно в GIF для просмотра, то потеря качества произойдет дважды при обоих преобразованиях. Тем не менее, выигрыш в размерах архивов зачастую настолько велик (в 3-20 раз!), а потери качества настолько малы, что хранение изображений в JPEG оказывается очень эффективным.

Несколько слов необходимо сказать о модификациях этого алгоритма. Хотя JPEG и является стандартом ISO, формат его файлов не был зафиксирован. Пользуясь этим, производители создают свои, несовместимые между собой форматы, и, следовательно, могут изменить алгоритм. Так, внутренние таблицы алгоритма, рекомендованные ISO, заменяются ими на свои собственные. Кроме того, легкая неразбериха присутствует при задании степени потерь. Например, при тестировании выясняется, что 'отличное' качество, '100%' и '10 баллов' дают существенно различающиеся картинки. При этом, кстати, '100%' качества не означают сжатие без потерь. Встречаются также варианты JPEG для специфических приложений.

Как стандарт ISO JPEG начинает все шире использоваться при обмене изображениями в компьютерных сетях. Поддерживается алгоритм JPEG в форматах Quick Time, PostScript Level 2, Tiff 6.0 и, на данный момент, занимает видное место в системах мультимедиа.

Идея метода

Фрактальная архивация основана на том, что мы представляем изображение в более компактной форме — с помощью коэффициентов системы итерируемых функций (Iterated Function System — далее по тексту как IFS). Прежде, чем рассматривать сам процесс архивации, разберем, как IFS строит изображение, т.е. процесс декомпрессии.

Строго говоря, IFS представляет собой набор трехмерных аффинных преобразований, в нашем случае переводящих одно изображение в другое. Преобразованию подвергаются точки в трехмерном пространстве (х_координата, у_координата, яркость).

Наиболее наглядно этот процесс продемонстрировал Барнсли в своей книге “Fractal Image Compression”. Там введено понятие Фотокопировальной Машины, состоящей из экрана, на котором изображена исходная картинка, и системы линз, проецирующих изображение на другой экран:

Линзы могут проецировать часть изображения произвольной формы в любое другое место нового изображения. Области, в которые проецируются изображения, не пересекаются. Линза может менять яркость и уменьшать контрастность. Линза может зеркально отражать и поворачивать свой фрагмент изображения. Линза должна масштабировать (уменьшать)свой фрагмент изображения.

Расставляя линзы и меняя их характеристики, мы можем управлять получаемым изображением. Одна итерация работы Машины заключается в том, что по исходному изображению с помощью проектирования строится новое, после чего новое берется в качестве исходного. Утверждается, что в процессе итераций мы получим изображение, которое перестанет изменяться. Оно будет зависеть только от расположения и характеристик линз, и не будет зависеть от исходной картинки. Это изображение называется “неподвижной точкой” или аттрактором данной IFS. Соответствующая теория гарантирует наличие ровно одной неподвижной точки для каждой IFS.

Поскольку отображение линз является сжимающим, каждая линза в явном виде задает самоподобные области в нашем изображении. Благодаря самоподобию мы получаем сложную структуру изображения при любом увеличении. Таким образом, интуитивно понятно, что система итерируемых функций задает фрактал (нестрого — самоподобный математический объект).

Наиболее известны два изображения, полученных с помощью IFS: “треугольник Серпинского” и “папоротник Барнсли”. “Треугольник Серпинского” задается тремя, а “папоротник Барнсли” четырьмя аффинными преобразованиями (или, в нашей терминологии, “линзами”). Каждое преобразование кодируется буквально считанными байтами, в то время как изображение, построенное с их помощью, может занимать и несколько мегабайт.

Далее приводятся основные определения и теоремы, на которых базируется фрактальная компрессия. Этот материал более детально и с доказательствами рассматривается в [3] и в [4].

Определение. Преобразование , представимое в виде

где a, b, c, d, e, f действительные числа и  называется двумерным аффинным преобразованием.

Определение. Преобразование , представимое в виде

где a, b, c, d, e, f, p, q, r, s, t, u действительные числа и  называется трехмерным аффинным преобразованием.

Определение. Пусть  — преобразование в пространстве Х. Точка  такая, что называется неподвижной точкой (аттрактором) преобразования.

Определение. Преобразование  в метрическом пространстве (Х, d) называется сжимающим, если существует число s: , такое, что

Замечание: Формально мы можем использовать любое сжимающее отображение при фрактальной компрессии, но реально используются лишь трехмерные аффинные преобразования с достаточно сильными ограничениями на коэффициенты.

Теорема. (О сжимающем преобразовании)

Пусть  в полном метрическом пространстве (Х, d). Тогда существует в точности одна неподвижная точка  этого преобразования, и для любой точки  последовательность  сходится к .

Более общая формулировка этой теоремы гарантирует нам сходимость.

Определение. Изображением называется функция S, определенная на единичном квадрате и принимающая значения от 0 до 1 или 

Пусть трехмерное аффинное преобразование , записано в виде

и определено на компактном подмножестве  декартова квадрата [0..1]x[0..1]. Тогда оно переведет часть поверхности S в область , расположенную со сдвигом (e,f) и поворотом, заданным матрицей

При этом, если интерпретировать значение S как яркость соответствующих точек, она уменьшится в p раз (преобразование обязано быть сжимающим) и изменится на сдвиг q.

Определение. Конечная совокупность W сжимающих трехмерных аффинных преобразований , определенных на областях , таких, что  и , называется системой итерируемых функций (IFS).

Системе итерируемых функций однозначно сопоставляется неподвижная точка — изображение. Таким образом, процесс компрессии заключается в поиске коэффициентов системы, а процесс декомпрессии — в проведении итераций системы до стабилизации полученного изображения (неподвижной точки IFS). На практике бывает достаточно 7-16 итераций. Области  в дальнейшем будут именоваться ранговыми, а области  — доменными.

Построение алгоритма

Как уже стало очевидным из изложенного выше, основной задачей при компрессии фрактальным алгоритмом является нахождение соответствующих аффинных преобразований. В самом общем случае мы можем переводить любые по размеру и форме области изображения, однако в этом случае получается астрономическое число перебираемых вариантов разных фрагментов, которое невозможно обработать на текущий момент даже на суперкомпьютере.

В учебном варианте алгоритма, изложенном далее, сделаны следующие ограничения на области:

1. Все области являются квадратами со сторонами, параллельными сторонам изображения. Это ограничение достаточно жесткое. Фактически мы собираемся аппроксимировать все многообразие геометрических фигур лишь квадратами.
2. При переводе доменной области в ранговую уменьшение размеров производится ровно в два раза. Это существенно упрощает как компрессор, так и декомпрессор, т.к. задача масштабирования небольших областей является нетривиальной.
3. Все доменные блоки — квадраты и имеют фиксированный размер. Изображение равномерной сеткой разбивается на набор доменных блоков.
4. Доменные области берутся “через точку” и по Х, и по Y, что сразу уменьшает перебор в 4 раза.
5. При переводе доменной области в ранговую поворот куба возможен только на 0⁰, 90⁰, 180⁰ или 270⁰. Также допускается зеркальное отражение. Общее число возможных преобразований (считая пустое) — 8.
6. Масштабирование (сжатие) по вертикали (яркости) осуществляется в фиксированное число раз — в 0,75.

1. Построить алгоритм, для которого требуется сравнительно малое число операций даже на достаточно больших изображениях.
2. Очень компактно представить данные для записи в файл. Нам требуется на каждое аффинное преобразование в IFS:

• два числа для того, чтобы задать смещение доменного блока. Если мы ограничим входные изображения размером 512х512, то достаточно будет по 8 бит на каждое число.
• три бита для того, чтобы задать преобразование симметрии при переводе доменного блока в ранговый.
• 7-9 бит для того, чтобы задать сдвиг по яркости при переводе.

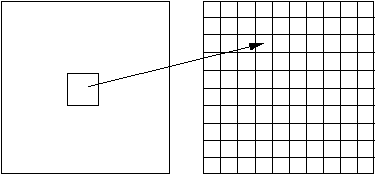
Например, для файла в градациях серого 256 цветов 512х512 пикселов при размере блока 8 пикселов аффинных преобразований будет 4096 (512/8x512/8). На каждое потребуется 3.5 байта. Следовательно, если исходный файл занимал 262144 (512х512) байт (без учета заголовка), то файл с коэффициентами будет занимать 14336 байт. Коэффициент архивации — 18 раз. При этом мы не учитываем, что файл с коэффициентами тоже может обладать избыточностью и архивироваться методом архивации без потерь, например LZW.

Отрицательные стороны предложенных ограничений:

1. Поскольку все области являются квадратами, невозможно воспользоваться подобием объектов, по форме далеких от квадратов (которые встречаются в реальных изображениях достаточно часто.)
2. Аналогично мы не сможем воспользоваться подобием объектов в изображении, коэффициент подобия между которыми сильно отличается от 2.
3. Алгоритм не сможет воспользоваться подобием объектов в изображении, угол между которыми не кратен 90⁰.

Сам алгоритм упаковки сводится к перебору всех доменных блоков и подбору для каждого соответствующего ему рангового блока. Ниже приводится схема этого алгоритма.

for (all range blocks) {
    min_distance = MaximumDistance;
    Rij = image->CopyBlock(i,j);
    for (all domain blocks) { // С поворотами и отр.
        current=Координаты тек. преобразования;
        D=image->CopyBlock(current);
        current_distance = Rij.L2distance(D);
        if(current_distance < min_distance) {
            // Если коэффициенты best хуже:
            min_distance = current_distance;
            best = current;
        }
    } //Next range
    Save_Coefficients_to_file(best);
} //Next domain

Как видно из приведенного алгоритма, для каждого рангового блока делаем его проверку со всеми возможными доменными блоками (в том числе с прошедшими преобразование симметрии), находим вариант с наименьшей мерой L₂ (наименьшим среднеквадратичным отклонением) и сохраняем коэффициенты этого преобразования в файл. Коэффициенты — это (1) координаты найденного блока, (2) число от 0 до 7, характеризующее преобразование симметрии (поворот, отражение блока), и (3) сдвиг по яркости для этой пары блоков. Сдвиг по яркости вычисляется как:

где r_ij — значения пикселов рангового блока (R), а d_ij — значения пикселов доменного блока (D). При этом мера считается как:

Мы не вычисляем квадратного корня из L₂ меры и не делим ее на n, поскольку данные преобразования монотонны и не помешают нам найти экстремум, однако мы сможем выполнять на две операции меньше для каждого блока.

Посчитаем количество операций, необходимых нам для сжатия изображения в градациях серого 256 цветов 512х512 пикселов при размере блока 8 пикселов:
 

Таким образом, нам удалось уменьшить число операций алгоритма компрессии до вполне вычисляемых (пусть и за несколько часов) величин.

Схема алгоритма декомпрессии изображений

Декомпрессия алгоритма фрактального сжатия чрезвычайно проста. Необходимо провести несколько итераций трехмерных аффинных преобразований, коэффициенты которых были получены на этапе компрессии.

В качестве начального может быть взято абсолютно любое изображение (например, абсолютно черное), поскольку соответствующий математический аппарат гарантирует нам сходимость последовательности изображений, получаемых в ходе итераций IFS, к неподвижному изображению (близкому к исходному). Обычно для этого достаточно 16 итераций.

Прочитаем из файла коэффициенты всех блоков;
Создадим черное изображение нужного размера;
Until(изображение не станет неподвижным){
    For(every range (R)){
        D=image->CopyBlock(D_coord_for_R);
        For(every pixel(i,j) in the block{
            Rij = 0.75Dij + oR;
        } //Next pixel
    } //Next block
}//Until end

Поскольку мы записывали коэффициенты для блоков Rij (которые, как мы оговорили, в нашем частном случае являются квадратами одинакового размера) последовательно, то получается, что мы последовательно заполняем изображение по квадратам сетки разбиения использованием аффинного преобразования.

Как можно подсчитать, количество операций на один пиксел изображения в градациях серого при восстановлении необычайно мало (N операций “+”, 1 операций “* ”, где N — количество итераций, т.е. 7-16). Благодаря этому, декомпрессия изображений для фрактального алгоритма проходит быстрее декомпрессии, например, для алгоритма JPEG, в котором на точку приходится (при оптимальной реализации операций обратного ДКП и квантования) 64 операции “+” и 64 операции “? ” (без учета шагов RLE и кодирования по Хаффману!). При этом для фрактального алгоритма умножение происходит на рациональное число, одно для каждого блока. Это означает, что мы можем, во-первых, использовать целочисленную рациональную арифметику, которая существенно быстрее арифметики с плавающей точкой. Во-вторых, умножение вектора на число — более простая и быстрая операция, часто закладываемая в архитектуру процессора (процессоры SGI, Intel MMX...), чем скалярное произведение двух векторов, необходимое в случае JPEG. Для полноцветного изображения ситуация качественно не изменяется, поскольку перевод в другое цветовое пространство используют оба алгоритма.

Оценка потерь и способы их регулирования

При кратком изложении упрощенного варианта алгоритма были пропущены многие важные вопросы. Например, что делать, если алгоритм не может подобрать для какого-либо фрагмента изображения подобный ему? Достаточно очевидное решение — разбить этот фрагмент на более мелкие, и попытаться поискать для них. В то же время понятно, что эту процедуру нельзя повторять до бесконечности, иначе количество необходимых преобразований станет так велико, что алгоритм перестанет быть алгоритмом компрессии. Следовательно, мы допускаем потери в какой-то части изображения.

Для фрактального алгоритма компрессии, как и для других алгоритмов сжатия с потерями, очень важны механизмы, с помощью которых можно будет регулировать степень сжатия и степень потерь. К настоящему времени разработан достаточно большой набор таких методов. Во-первых, можно ограничить количество аффинных преобразований, заведомо обеспечив степень сжатия не ниже фиксированной величины. Во-вторых, можно потребовать, чтобы в ситуации, когда разница между обрабатываемым фрагментом и наилучшим его приближением будет выше определенного порогового значения, этот фрагмент дробился обязательно (для него обязательно заводится несколько “линз”). В-третьих, можно запретить дробить фрагменты размером меньше, допустим, четырех точек. Изменяя пороговые значения и приоритет этих условий, мы будем очень гибко управлять коэффициентом компрессии изображения в диапазоне от побитового соответствия до любой степени сжатия. Заметим, что эта гибкость будет гораздо выше, чем у ближайшего “конкурента” — алгоритма JPEG.

Английское название рекурсивного сжатия — wavelet. На русский язык оно переводится как волновое сжатие, и как сжатие с использованием всплесков. Этот вид архивации известен довольно давно и напрямую исходит из идеи использования когерентности областей. Ориентирован алгоритм на цветные и черно-белые изображения с плавными переходами. Идеален для картинок типа рентгеновских снимков. Коэффициент сжатия задается и варьируется в пределах 5-100. При попытке задать больший коэффициент на резких границах, особенно проходящих по диагонали, проявляется “лестничный эффект” — ступеньки разной яркости размером в несколько пикселов.

Идея алгоритма заключается в том, что мы сохраняем в файл разницу — число между средними значениями соседних блоков в изображении, которая обычно принимает значения, близкие к 0.

Так два числа a_2i и a_2i+1 всегда можно представить в виде b¹_i=(a_2i+a_2i+1)/2 и b²_i=(a_2i-a_2i+1)/2. Аналогично последовательность a_i может быть попарно переведена в последовательность b^1,2_i.

Разберем конкретный пример: пусть мы сжимаем строку из 8 значений яркости пикселов (a_i): (220, 211, 212, 218, 217, 214, 210, 202). Мы получим следующие последовательности b¹_i, и b²_i: (215.5, 215, 215.5, 206) и (4.5, -3, 1.5, 4). Заметим, что значения b²_i достаточно близки к 0. Повторим операцию, рассматривая b¹_i как a_i. Данное действие выполняется как бы рекурсивно, откуда и название алгоритма. Мы получим из (215.5, 215, 215.5, 206): (215.25, 210.75) (0.25, 4.75). Полученные коэффициенты, округлив до целых и сжав, например, с помощью алгоритма Хаффмана с фиксированными таблицами, мы можем поместить в файл.

Заметим, что мы применяли наше преобразование к цепочке только два раза. Реально мы можем позволить себе применение wavelet- преобразования 4-6 раз. Более того, дополнительное сжатие можно получить, используя таблицы алгоритма Хаффмана с неравномерным шагом (т.е. нам придется сохранять код Хаффмана для ближайшего в таблице значения). Эти приемы позволяют достичь заметных коэффициентов сжатия.

Используя эти формулы, мы для изображения 512х512 пикселов получим после первого преобразования 4 матрицы размером 256х256 элементов:
 

В первой, как легко догадаться, будет храниться уменьшенная копия изображения. Во второй — усредненные разности пар значений пикселов по горизонтали. В третьей — усредненные разности пар значений пикселов по вертикали. В четвертой — усредненные разности значений пикселов по диагонали. По аналогии с двумерным случаем мы можем повторить наше преобразование и получить вместо первой матрицы 4 матрицы размером 128х128. Повторив наше преобразование в третий раз, мы получим в итоге: 4 матрицы 64х64, 3 матрицы 128х128 и 3 матрицы 256х256. На практике при записи в файл, значениями, получаемыми в последней строке (), обычно пренебрегают (сразу получая выигрыш примерно на треть размера файла — 1- 1/4 - 1/16 - 1/64...).

К достоинствам этого алгоритма можно отнести то, что он очень легко позволяет реализовать возможность постепенного “прояв–ления” изображения при передаче изображения по сети. Кроме того, поскольку в начале изображения мы фактически храним его уменьшенную копию, упрощается показ “огрубленного” изображения по заголовку.

В отличие от JPEG и фрактального алгоритма данный метод не оперирует блоками, например, 8х8 пикселов. Точнее, мы оперируем блоками 2х2, 4х4, 8х8 и т.д. Однако за счет того, что коэффициенты для этих блоков мы сохраняем независимо, мы можем достаточно легко избежать дробления изображения на “мозаичные” квадраты.

В заключение рассмотрим таблицы, в которых сводятся воедино параметры различных алгоритмов сжатия изображений, рассмотренных нами выше.

1. ориентация на фотореалистичные изображения с 16 миллионами цветов (24 бита);
2. использование сжатия с потерями, возможность за счет потерь регулировать качество изображений;
3. использование избыточности изображений в двух измерениях;
4. появление существенно несимметричных алгоритмов;
5. увеличивающаяся степень сжатия изображений.

В чем разница между алгоритмами с потерей информации и без потери информации? Приведите примеры мер потери информации и опишите их недостатки. За счет чего сжимает изображения алгоритм JPEG? В чем заключается идея фрактального алгоритма компрессии? В чем заключается идея рекурсивного (волнового) сжатия? Можно ли применять прием перевода в другое цветовое пространство алгоритма JPEG в других алгоритмах компрессии?
Сравните приведенные в этой главе алгоритмы сжатия изображений.

• Общие положения алгоритмов сжатия изображений
• Введение
• Классы изображений
• Классы приложений
• Критерии сравнения алгоритмов
• Контрольные вопросы к разделу
• Алгоритмы архивации без потерь
• Алгоритм RLE
• Алгоритм LZW
• Алгоритм Хаффмана
• JBIG
• Lossless JPEG
• Заключение
• Контрольные вопросы к разделу
• Алгоритмы архивации с потерями
• Проблемы алгоритмов архивации с потерями
• Алгоритм JPEG
• Фрактальный алгоритм
• Рекурсивный (волновой) алгоритм
• Заключение
• Контрольные вопросы к разделу
• Различия между форматом и алгоритмом
• Литература
• Литература по алгоритмам сжатия
• Литература по форматам изображений
• Приложение. Таблицы сравнения алгоритмов
• Архивация двуцветного изображения
• Архивация 16-цветного изображения
• Архивация изображения в градациях серого
• Архивация полноцветного изображения
• Архивация полноцветного изображения в 100 раз
• Приложение. Апплет, обеспечивающий фрактальную декомпрессию
• Ссылки на ресурсы по сжатию изображений в сети