К разделу 'Сжатие изображений' сайта AlgoList.

  • Л. Левкович-Маслюк, А. Переберин.
     

      Введение в Вейвлет-Анализ



     




      Лекция 1
    Ортогональные вейвлеты и многомасштабный анализ



      Введение


    Вейвлет-преобразование естественно возникает в контексте многомасштабного анализа (multiresolution analysis), МА. МА – это математическая конструкция, синтезирующая две идеи обработки сигналов. Первая идея – разложение сигнала по поддиапазонам (subband decomposition) при помощи квадратурных зеркальных фильтров (quadrature mirror filters) – появилась в задаче сжатия речи. Вторая идея – пирамидное представление (pyramid representation) – в задаче сжатия изображений. Обе идеи связаны с применением к сигналу фильтров специального вида. В первом случае теория строилась в терминах Фурье-преобразования сигнала, во втором – в терминах исходного сигнала.

    Рассмотрим сигнал – последовательность чисел x=. Для сглаживания сигнала, подавления шума и других целей часто используют фильтры – преобразования свертки вида:

    .

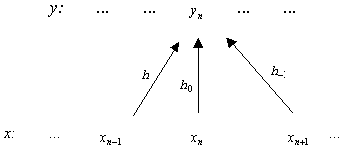
    Сигнал y= получается “локальным усреднением” сигнала x с помощью набора “весов” :

    В дальнейшем нам понадобятся следующие понятия.
     

    • Дискретное преобразование Фурье (ДПФ) сигнала: 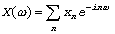 (формальная сумма).
    • z-преобразование сигнал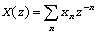а: (формальная сумма).
     
    • Преобразование Фурье функции 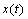имеет вид .
    В этих терминах применение фильтра записывается так:

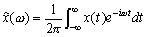    (1.1)

    ,

    или

    (1.1')

    (если сигнал конечен, его обычно доопределяют периодическим образом для всех целых значений индекса).
     

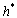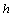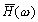    • Транспонированный фильтр состоит из тех же коэффициентов, что и фильтр , переставленных в обратном порядке. В Фурье-области транспонированный фильтр имеет вид . Коэффициенты всех сигналов и фильтров будут предполагаться вещественными.