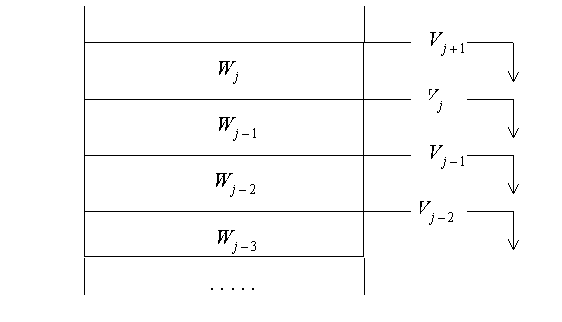
К разделу 'Сжатие изображений' сайта AlgoList.

Л. Левкович-Маслюк, А. Переберин. Введение в вейвлет-анализ

  Ортогональный многомасштабный анализ


Концепция МА дает схему представления сигналов, синтезирующую рассмотренные выше методы. Сначала опишем эту схему неформально.

Вклад пирамидного представления: пространство функций (сигналов) исчерпывается системой вложенных подпространств (аналог ПГ). Каждое из них порождено целочисленными сдвигами одной и той же функции , растянутой в  раз. Эта функция является решением уравнения (1.4). Для каждого подпространства n фиксировано, и характеризует масштаб. Задача состоит в том, чтобы разложить сигнал на его “грубую” крупномасштабную версию и набор “деталей” (аналог ПЛ), отличающих версии промежуточных масштабов друг от друга.

Вклад техники разложения по поддиапазонам: коэффициенты h должны быть такими, чтобы фильтр  удовлетворял условиям (1.2’). Оказывается, в этом случае процесс перехода от более тонкой к более грубой версии сигнала сводится к применению фильтра , а вычисление “деталей” – к применению фильтра .

Вклад самой схемы МА в эту картину таков: оказывается, что при выполнении предыдущих условий пространства “деталей” устроены аналогично пространствам разномасштабных версий. А именно, существует такая функция , порождающая эти пространства своими сдвигами и растяжениями. Эта функция выражается через функцию  по формуле, похожей на (1.4):

 (1.5)

Функция называется ортогональным вейвлетом.

Теперь дадим более строгие определения. В качестве пространства сигналов будем рассматривать  – пространство комплекснозначных функций  на прямой, для которых . В этом пространстве определено скалярное произведение функций по формуле . Число  называется нормой функции . Базисом в пространстве  называется такая система функций , что любая функция единственным образом записывается в виде . Базис называется ортонормированным, если . В этом случае .

Популярный пример ортобазиса (правда, в пространстве периодических функций) – базис Фурье . В пространстве  также есть много классических базисов – Эрмита, Лаггера и др. Многомасштабный анализ есть не что иное, как разложение данной функции (сигнала) в ортобазисе, порожденном сдвигами и растяжениями ортогонального вейвлета.

Определение. Ортогональным многомасштабным анализом (ОМА) в пространстве  называется система подпространств , удовлетворяющая следующим условиям.
 

  1. ,
  2. ,
  3. ,
  4. ,
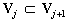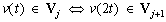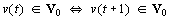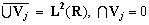  5. существует 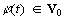такая, что функции 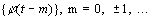 образуют ортонормированный базис пространства .
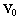Функция называется скейлинг-функцией (scaling function).

Пример. Пусть на интервале  и  вне этого интервала. Тогда  состоит из функций, постоянных на интервалах вида ,  – из функций, постоянных на интервалах вида ,  – из функций, постоянных на интервалах вида , и т.д.

Будем считать, что пространство  состоит из сигналов, заданных “с разрешением 1”. Тогда пространство  – сигналы, заданные с разрешением . Любое  отличается от  только перемасштабированием. Поэтому пространство  порождено ортобазисом . Например, порождено функциями вида . Т.к. , функция  обязана линейно выражаться через сдвиги . Значит, существуют такие коэффициенты , что  Это в точности уравнение (1.4). Скейлинг-функция – это эквивалентная весовая функция из пирамидного представления.

Можно предположить, что изначально заданный сигнал  известен с разрешением 1, другими словами, , и нам даны коэффициенты  его разложения по сдвигам скейлинг-функции:

Естественно считать версией масштаба 2 ортогональную проекцию на подпространство . Она задается набором скалярных произведений с функциями из ортобазиса , то есть величинами . Из уравнения (1.4) и условий ортогональности имеем:

(1.6)

Другими словами, проекция осуществляется путем свертки с фильтром и прореживания вдвое. Заметим, что прореживание вдвое “встроено” в эту формулу (через индекс ). Разумеется, это следствие выбора базиса в .

В качестве деталей сигнала , исчезающих при переходе к масштабу 2, следует взять компоненту , ортогональную к сигналам масштаба 2, т.е. к пространству . Имеет место разложение , где для любых функций  выполнено . Замечательно, что ортобазисом  будет набор функций , где  задается формулой (1.5). Коэффициенты  имеют вид , что эквивалентно формуле (1.3). Искомая проекция задается набором скалярных произведений с функциями из ортобазиса , то есть величинами . Совершенно аналогично (1.6) получаем

(1.6’)

что равносильно свертке с фильтром  и прореживанию вдвое. Та же схема действует на любом масштабе. При любом j , ортобазисом  будет и разложение сигнала из на сглаженную часть и детали (т.е. его проекции на и ) находятся по формулам (1.6) и (1.6’). Совокупность же функций , где j и m пробегают все целые значения, будет базисом всего пространства .

Тем самым, ортогональность базисных функций ОМА приводит к тому, что вычисление сглаженных версий сигнала и его деталей выполняется сверткой с парой квадратурных зеркальных фильтров.

Продолжение примера. В данном случае . Другими словами, с точностью до нормировки коэффициенты проекции на  являются суммами значений кусочно-постоянной функции на соседних единичных интервалах, а коэффициенты проекции на пространство деталей  – разностями этих значений. Функция  равна 1 на интервале , –1 на интервале , и нулю во всех остальных точках. Множество функций  образует ортонормированный базис всего пространства . Это классический базис Хаара.

Итак, ОМА позволяет построить аналог ПГ и ПЛ, пользуясь квадратурными зеркальными фильтрами. Перепишем теперь формулы (1.6) и (1.6’) в матричном виде. Введем матрицы H и G:

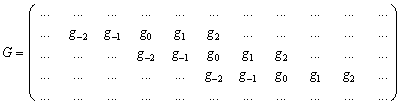
Тогда условия точного восстановления (1.2) дают условие на матрицы H и G: 

(1.7)

Обозначив вектор исходных коэффициентов через x, можно записать его разложение в сумму огрубленной версии и серии векторов деталей:

(1.8)

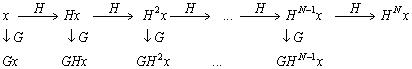
Эту процедуру иногда называют быстрым вейвлет-преобразованием (Fast Wavelet Transform), а иногда – алгоритмом Малла (Mallat algorithm). Число итераций N может быть произвольным. Если вектор x конечен, его надо продолжить “на бесконечность”; проще всего это сделать периодическим образом. Каждое применение операторов H и G сокращает длину вектора вдвое, поэтому общее число операций линейно по длине входа.

Результатом преобразования является набор векторов . Обратное преобразование делается по такой схеме:
 
(1.9)

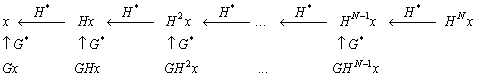
На первом шаге восстанавливается  по формуле , которая верна в силу (1.7). Затем вычисляется , и т.д.

Рисунок 4. ОМА в .