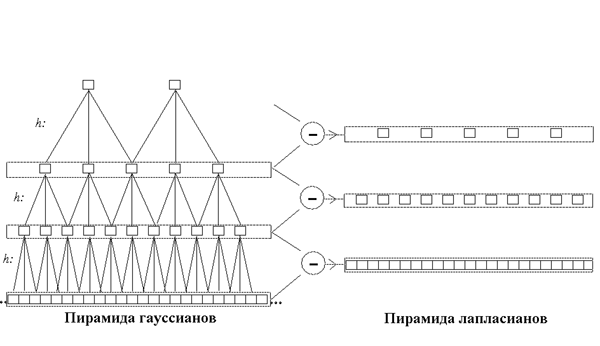
На рис.2 схематически изображено пирамидное представление одномерного сигнала. Сигналу ставятся в соответствие две пирамиды: пирамида гауссианов (ПГ) и пирамида лапласианов (ПЛ). Эти названия отражают аналогию с популярными в графике операциями сглаживания (свертки с колоколообразным фильтром) и выделения перепадов (вычисления “дискретного оператора Лапласа”). Можно считать эту конструкцию упрощенным вариантом предыдущей.

В основании ПГ находится исходный сигнал. Следующий этаж ПГ – исходный сигнал, профильтрованный низкочастотным фильтром h и прореженный после этого вдвое – предполагается, что фильтр h “убивает” верхнюю половину частотного диапазона, поэтому густоту выборки можно соответственно уменьшить. К этому этажу применяется та же операция, и так далее. В случае конечных сигналов каждый следующий этаж вдвое короче предыдущего.

Этажи ПЛ – разности между последовательными этажами ПГ. Они вычисляются так. Пусть, например,  и  – первый и второй этажи ПГ,  – первый этаж ПЛ, который мы хотим вычислить. Для этого сначала выравниваются длины этажей:

а затем выполняется фильтрация сопряженным фильтром  (его коэффициенты – переставленные в обратном порядке коэффициенты h, в Фурье-области это равнозначно переходу к ). В результате возникает вектор  . По определению,

.

Теперь вместо исходного сигнала () достаточно запомнить пару (). Исходный сигнал можно точно восстановить по формуле:

Сигнал  вдвое короче исходного, а сигнал , как правило, почти целиком состоит из очень малых величин. Многие из этих величин можно без заметного ущерба для точности восстановления заменить нулями, а остальные закодировать более короткими словами, чем компоненты исходного сигнала. За счет этого общая длина записи () будет существенно меньше длины записи исходного сигнала. Это сокращение станет еще больше, если вычислить несколько этажей ПЛ, и запоминать вместо исходного сигнала несколько этажей ПЛ и последний этаж ПГ.

Степень сжатия информации этим методом зависит от выбора фильтра h. При экспериментах с пирамидными представлениями было сделано наблюдение: “качество” фильтра удобно выражать в терминах эквивалентной весовой функции. Эта функция возникает так. Нетрудно вычислить коэффициенты фильтров, свертка сигнала с которыми дает сразу второй этаж ПГ, третий этаж, и т.д. 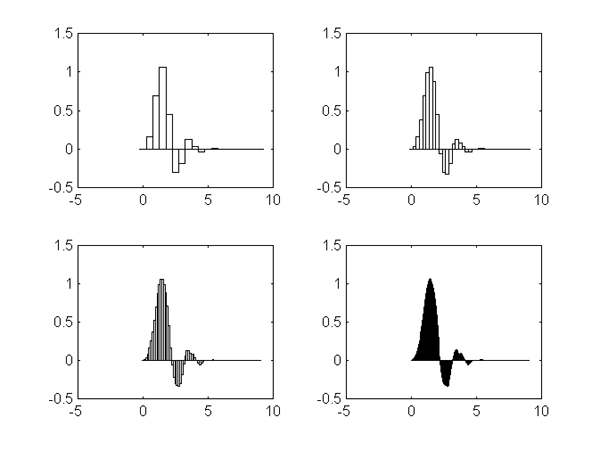Оказывается, что при соответствующей нормировке векторы этих коэффициентов сходятся к некоей предельной “форме” – графику функции , которая должна удовлетворять функциональному уравнению:

(1.4)

Процесс получения  изображен на рис. 3.