Биортогональный многомасштабный анализ
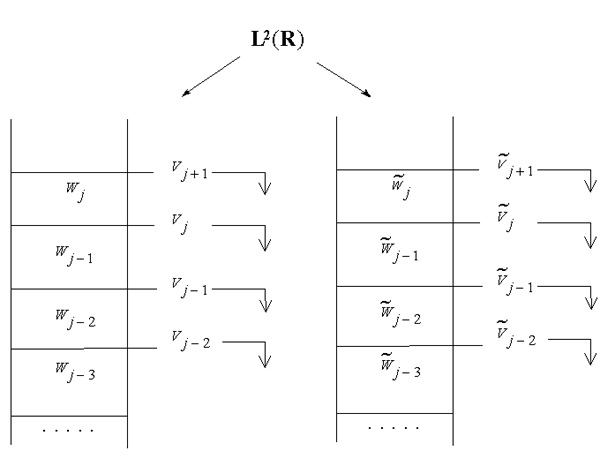
Существует более гибкая конструкция МА, где класс допустимых фильтров шире, их коэффициенты проще вычислить, они могут быть симметричными и обладать другими полезными свойствами. Это – биортогональный МА, БМА. Быстрый алгоритм Малла сохраняется, но при разложении и восстановлении используются разные пары фильтров. Каждой паре соответствует МА со своими скейлинг-функцией и вейвлетом. Но эти МА не ортогональны – сдвиги скейлинг-функций и вейвлетов не ортогональны друг другу. Поэтому преобразования (1.8) – (1.9) не ортогональны. (Это означает, между прочим, что погрешность, внесенная при сжатии, может увеличиваться при восстановлении).
Рассмотрим две пары фильтров: ![]() и
и ![]() . Мы
хотим проводить разложение при помощи свертки с
. Мы
хотим проводить разложение при помощи свертки с ![]() ,
а восстановление – при помощи
,
а восстановление – при помощи ![]() (в ортогональном случае
(в ортогональном случае ![]() ).
Запишем условия точного восстановления (см. начало лекции 1). В терминах
).
Запишем условия точного восстановления (см. начало лекции 1). В терминах ![]() -преобразования
разложение на высокие и низкие частоты с прореживанием вдвое имеет вид:
-преобразования
разложение на высокие и низкие частоты с прореживанием вдвое имеет вид:
Записав в аналогичном виде процесс восстановления с помощью пары ![]() ,
приравняв результат к
,
приравняв результат к ![]() ,
и подставив
,
и подставив ![]() ,
получим условия на ДПФ искомых фильтров (аналог (1.2)) :
,
получим условия на ДПФ искомых фильтров (аналог (1.2)) :
(2.7)
Вводя матрицы
запишем эти условия в виде:
(2.7’)
Их решения ищутся при помощи такого итерационного процесса (см. рис.
3 из лекции 1): сначала в правую часть подставляется единичная ступенька
(скейлинг-функция Хаара), затем – результат этой подстановки, сжатый вдвое
по ![]() , и
т.д. Мы видели, что предельная функция определяет ОМА только если
, и
т.д. Мы видели, что предельная функция определяет ОМА только если ![]() имеет очень специальный вид (см. 2.3 – 2.6). Для БМА выбор возможных фильтров
шире, но тоже требуются дополнительные условия, при которых имеет место
сходимость итераций, а предельные функции образуют базис. Предположим,
что все эти условия выполнены, и определим биортогональные вейвлеты формулами:
имеет очень специальный вид (см. 2.3 – 2.6). Для БМА выбор возможных фильтров
шире, но тоже требуются дополнительные условия, при которых имеет место
сходимость итераций, а предельные функции образуют базис. Предположим,
что все эти условия выполнены, и определим биортогональные вейвлеты формулами:
Функции ![]()
![]() ,
, ![]() называют основными (primary), функции
называют основными (primary), функции ![]() ,
, ![]() – дуальными (dual). Взаимосвязь основных и дуальных функций, вытекающая
из (2.7), такова: при всех целых
– дуальными (dual). Взаимосвязь основных и дуальных функций, вытекающая
из (2.7), такова: при всех целых ![]()
(2.10)
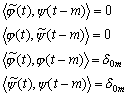
![]() (
(![]() )
не обязаны быть ортогональными к
)
не обязаны быть ортогональными к ![]() (
(![]() ). Однако возможен
такой случай, когда базисы из сдвигов скейлинг-функций и вейвлетов в каждом
из этих подпространств не ортогональны, а сами подпространства ортогональны;
такой МА называется полуортогональным (semiorthogonal).
). Однако возможен
такой случай, когда базисы из сдвигов скейлинг-функций и вейвлетов в каждом
из этих подпространств не ортогональны, а сами подпространства ортогональны;
такой МА называется полуортогональным (semiorthogonal).
В случае ОМА для сигналов вида ![]() коэффициенты их проекций на
коэффициенты их проекций на ![]() и
и ![]() давались
формулами (1.6) и (1.6’) так как базисы сдвигов скейлинг-функций и вейвлетов
были ортогональны. В случае БМА коэффициенты разложения сигнала по основным
функциям – это скалярные произведения сигнала с дуальными функциями:
давались
формулами (1.6) и (1.6’) так как базисы сдвигов скейлинг-функций и вейвлетов
были ортогональны. В случае БМА коэффициенты разложения сигнала по основным
функциям – это скалярные произведения сигнала с дуальными функциями:
Поэтому, чтобы спроектировать сигнал на ![]() ,
надо вычислить его скалярные произведения с базисными функциями
,
надо вычислить его скалярные произведения с базисными функциями ![]() ,
а на
,
а на ![]() –
с базисными функциями
–
с базисными функциями ![]() .
Коэффициенты соответствующих разложений имеют вид:
.
Коэффициенты соответствующих разложений имеют вид:
(2.11)
В лекции 1 были введены матрицы ![]() и
и ![]() ; определив
аналогичным образом
; определив
аналогичным образом ![]() и
и ![]() ,
получим условие точного восстановления в виде:
,
получим условие точного восстановления в виде:
(2.12)
Схемы разложения и восстановления получаются из (1.8) – (1.9) заменой
операторов разложения на ![]() и
и ![]() .
.
В заключение этого раздела приведем популярный пример серии биортогональных
МА, где ![]() и
и ![]() являются
сплайнами. Достаточно построить
являются
сплайнами. Достаточно построить ![]() и
и ![]() , удовлетворяющие
условию
, удовлетворяющие
условию
и положить
Как и в ортогональном случае, должны выполняться некоторые дополнительные
условия (которые мы здесь не уточняем), гарантирующие сходимость, регулярность
и базисность решений уравнений рескейлинга (2.8) – (2.9). Кроме того, желательно,
чтобы вейвлет, используемый для разложения (т.е. ![]() ),
имел хоть несколько нулевых моментов, а вейвлет и скейлинг-функция,
используемые для восстановления (
),
имел хоть несколько нулевых моментов, а вейвлет и скейлинг-функция,
используемые для восстановления (![]() и
и ![]() ) были
как можно более гладкими. Имеется решение, удовлетворяющее всем этим требованиям.
Это решение использует сомножители того тригонометрического многочлена,
который был использован для построения ОМА (см 2.5).
) были
как можно более гладкими. Имеется решение, удовлетворяющее всем этим требованиям.
Это решение использует сомножители того тригонометрического многочлена,
который был использован для построения ОМА (см 2.5).
Семейство фильтров имеет вид:
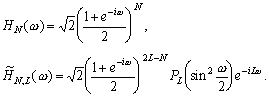
Скейлинг-функция ![]() является B-сплайном. На рис.2 показаны скейлинг-функции и вейвлеты БМА,
полученного при
является B-сплайном. На рис.2 показаны скейлинг-функции и вейвлеты БМА,
полученного при ![]() .
.
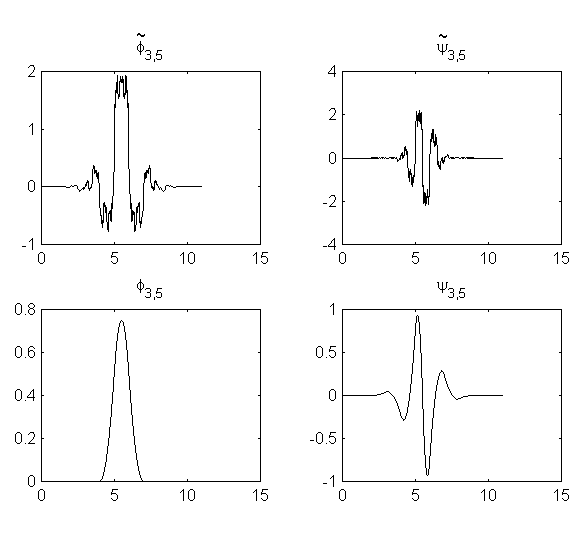
Ясно, что гладкость функций, порождающих дуальный МА, очень низка. При увеличении L получаются более гладкие функции, однако и длина фильтров соответственно увеличивается.