Л. Левкович-Маслюк,
А. Переберин. Введение в вейвлет-анализ
Вейвлет-пакеты
Для увеличения разрешения вейвлет-фильтров по частоте используется простой, красивый и эффективный прием. Опишем его для ортогонального случая. Напомним, что при работе алгоритма Малла на каждом шаге “отрезается” половина (в случае идеального фильтра) низкочастотной части диапазона. Но ведь можно применить ту же операцию “расщепления” (splitting) к любой из получающихся высокочастотных компонент. На рисунке 3 слева показана схема алгоритма Малла, справа – другая схема разложения сигнала, при которой каждый высокочастотный диапазон из схемы Малла тоже делится пополам.
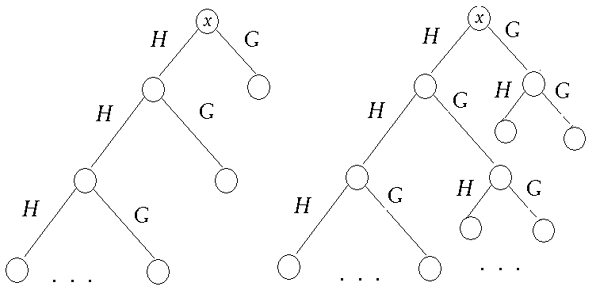
Похожую схему мы видели в самом начале первой лекции, когда говорили
о квадратурных зеркальных фильтрах. Теперь ей можно дать истолкование на
языке вейвлетов. Дерево на рис. 3 справа соответствует замене вейвлета 
на два новых вейвлета: 
и 
. Теперь
разложение 
превращается
в 
, где 
и 
порождены
соответственно 
и 
. Новые
вейвлеты тоже локализованы в пространстве, но на вдвое более широком отрезке,
чем исходный вейвлет, так как их локализация по частоте вдвое тоньше.
Можно нарисовать произвольное бинарное дерево разложения, и ему будет соответствовать набор подпространств с базисами, построенными по аналогичному рецепту. Функции, порождающие эти базисы, и называются вейвлет-пакетами (wavelet-packets). Ясно, что та же схема действует и в биортогональном случае.
На практике (при сжатии данных, например) мы имеем дело только с фильтрами. За счет выбора оптимального дерева для данного сигнала или класса сигналов иногда можно существенно (в несколько раз) повысить эффективность сжатия. Для выбора [квази]оптимального дерева разработан ряд методов. Все они основаны на введении некоторой функции (“энтропии”), позволяющей оценить “информативность” набора коэффициентов. Стратегия такова: сначала строится полное дерево разложения, затем снизу вверх анализируются пары узлов, имеющих общий корень. Если при переходе от корня к узлам энтропия не уменьшается, эта пара заменяется на корень. Упрощенный вариант – подобрать оптимальный уровень, т.е. высоту полного дерева, при которой энтропия минимальна.