Л. Левкович-Маслюк,
А. Переберин. Введение в вейвлет-анализ
Двумерный случай
Для ряда задач, например, для обработки растровых изображений, необходимо обрабатывать двумерные массивы данных. Многомасштабный анализ должен строиться в пространстве функций двух переменных. Существует несколько способов обобщить изложенные ранее конструкции на функции нескольких переменных (мы будем говорить только о функциях двух переменных).
Самый простой и широко распространенный путь – тензорное произведение одномерных МА. В качестве двумерной скейлинг-функции берется
.Вместо одного вейвлета возникает три:
(L означает низкую частоту, H
– высокую частоту). Пространства 
порождаются сдвигами скейлинг – функции на одном и том же масштабе:
пространства деталей имеют вид:
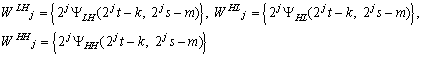
Соответствующие проекции находятся применением фильтров (в очевидных обозначениях):
,где x – двумерный сигнал. Классическая схема Малла предполагает рекурсивное применение той же процедуры к низкочастотной составляющей. На рисунке 4 показаны результаты двух шагов этого процесса для фотографии Ингрид Добеши (Ingrid Daubechies), внесшей выдающийся вклад в теорию вейвлет-анализа. Коэффициенты расположены по правилу:
Например, LH означает, что в этом квадранте стоит результат применения фильтра низких частот к столбцам, высоких частот – к строчкам исходной матрицы, и прореживания вдвое по каждому направлению. На рисунке 4а более ярким цветом обозначены коэффициенты большей амплитуды. Четко видно, что их положение указывает на резкие перепады яркости. Такие перепады являются наиболее информативными при беглом просмотре любого изображения. Вейвлет-представление позволяет их локализовать путем последовательного уточнения, начиная с более крупных масштабов. Кроме того, коэффициенты проекции на различные пространства деталей отвечают за перепады яркости различной ориентации: например, если фильтр высоких частот применялся к строчкам, то в соответствующем квадранте ярче выделены вертикальные перепады. Это хорошо видно на рисунке 4б.
