Л. Левкович-Маслюк,
А. Переберин. Введение в вейвлет-анализ
Сжатие изображений
Самый простой подход к сжатию изображений при помощи вейвлет-преобразования состоит в следующем:
- Выполнить вейвлет-преобразование.
- Упорядочить коэффициенты .
- Отбросить “хвост” упорядоченного массива, энергия которого равна допустимой (по условиям задачи) величине.
- Запомнить сохраненные коэффициенты и их положение в массиве исходных коэффициентов.
- При восстановлении заменять отброшенные коэффициенты нулями.
Однако существуют и более изощренные методы, где кодирование сразу идет на уровне битов. Один из них мы сейчас кратко опишем. Он является модификацией метода погруженного нуль-дерева (embedded zero-tree).
- Коэффициенты вейвлет-преобразования квантуются и записываются целыми числами.
- Строится упорядоченная таблица коэффициентов: сначала идут те, у которых в старшем двоичном разряде 1, затем – те, у которых в старшем разряде 0, но в следующем – 1, и т.д. В битовом представлении таблица выглядит так:
| s | s | s | s | s | s | s | s | s | s |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.. |
|
|
1 | 1 | 1 | 1 | 1 | 0 | 0 | 0.. | |
|
|
1 | 1 | 1.. | ||||||
|
|
|||||||||
В первой строке стоят знаки коэффициентов, во второй – старшие биты, и т.д. Ясно, что для воспроизведения исходного изображения достаточно запомнить (передать) только те биты, которые стоят в клетках, помеченных стрелками, а также длину стрелок и положение самих коэффициентов в исходном двумерном массиве коэффициентов. При передаче битов в таком порядке сначала передается самая существенная информация (старшие биты самых больших коэффициентов), потом менее существенная, и т.д. Этот процесс можно оборвать, дойдя до той части таблицы, где стоят “маленькие” коэффициенты. Проблема в том, как компактно передать таблицу положений сохраненных коэффициентов. Заметим, что полностью упорядочивать массив коэффициентов (по абсолютной величине) не надо, достаточно найти разбиение на группы, показанные в таблице, т.е на такие группы, что для фиксированного n
(2.13)
.
Фиксируем n,
и начинаем по очереди просматривать
на наличие значимых коэффициентов – т.е., удовлетворяющих (2.13).
Если в
есть значимые коэффициенты, это множество разбивается на некоторые подмножества,
и они опять проверяются на значимость, и т.д. Хорошо было бы построить
разбиение так, чтобы значимые множества состояли (почти всегда) из единственного
элемента, а незначимые были большими.
Именно здесь используется специфика вейвлет-анализа. В разложениях такого типа, как на рис. 4а, массив коэффициентов распадется на набор поддеревьев:
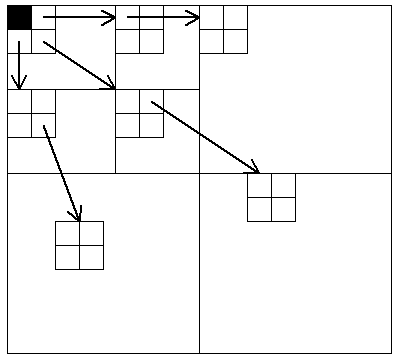
Верхний левый квадрант распадается на четверки коэффициентов. В каждой четверке три коэффициента (кроме закрашенного черным) имеют “отпрысков” – четверки коэффициентов на нижних уровнях; каждый из коэффициентов в этих четверках имеет своих отпрысков, и т.д. Узлу (i,j) соответствуют отпрыски с координатами (2i,2j), (2i,2j+1), (2i+1,2j), (2i+1,2j+1). В качестве изначального разбиения берется именно этот набор поддеревьев. Многие из них действительно состоят только из несущественных коэффициентов, так как малые значения на верхних уровнях почти всегда соответствуют малым значениям на нижних уровнях (если двигаться по направлению стрелок на рис. 5). Не углубляясь в дальнейшие подробности, отметим еще одну особенность этого красивого алгоритма: передается (запоминается) не таблица положений коэффициентов, а ключевые шаги процесса сортировки, что существенно компактнее (при декодировании этот процесс фактически воспроизводится в обратном порядке). Так как обычно многие поддеревья оказываются “нулевыми”, шагов сортировки будет не очень много.