К разделу 'Сжатие изображений' сайта AlgoList.

Л. Левкович-Маслюк, А. Переберин. Вейвлет-анализ и его приложения

  Мультивейвлеты


Мультивейвлеты (multiwavelets) – это векторнозначное обобщение вейвлетов. Они предназначены для разложения “многоканальных” сигналов, имеющих не одну, а несколько компонент. Впрочем, к такому виду можно привести и скалярный сигнал (переходом к четным и нечетным компонентам, например).

Мультивейвлеты определяются точно такими же (внешне!) уравнениями рескейлинга, что и обычные вейвлеты.

, 

Их привлекательность том, что они:

  • Как и обычные вейвлеты, порождают МА.
  • Сильнее локализованы в пространстве, что может оказаться удобно в ряде задач (например, в матфизике).
  • Допускают быстрый алгоритм преобразования (алгоритм Малла с матричными коэффициентами дословно переносится на этот случай)
Однако построить мультивейвлеты оказалось сложнее, чем обычные вейвлеты. Дело в том, что уравнения скейлинга имеют матричные коэффициенты, которые не коммутируют между собой. Поэтому найти подходящий набор коэффициентов, дающий гладкие решения уравнения рескейлинга, довольно сложно. Первый пример ортогональных и непрерывных мультивейвлетов получен Джеронимо, Хардином и Массопустом (Geronimo, Hardin, Massopust – GHM). Скейлинг-функции и вейвлеты в их примере были кусочно-самоподобными, и пример был построен с использованием методов из теории ИФС (итерационных функциональных систем), порождающих, вообще говоря, фрактальные функции. GHM-мультивейвлеты и скейлинг-функции показаны на рисунках 1 и 2:
Рисунок 1. Скейлинг – функции GHM.
 
Рисунок2. Мультивейвлеты GHM.

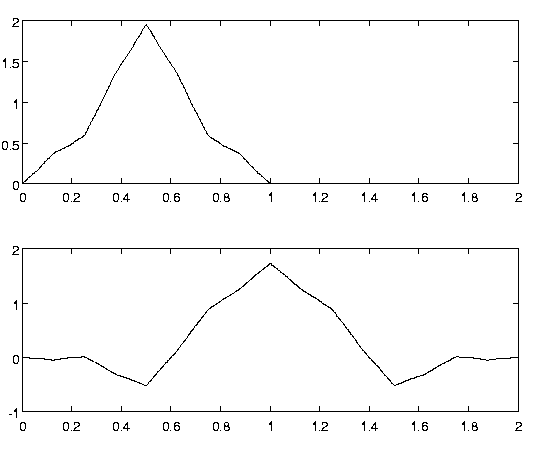
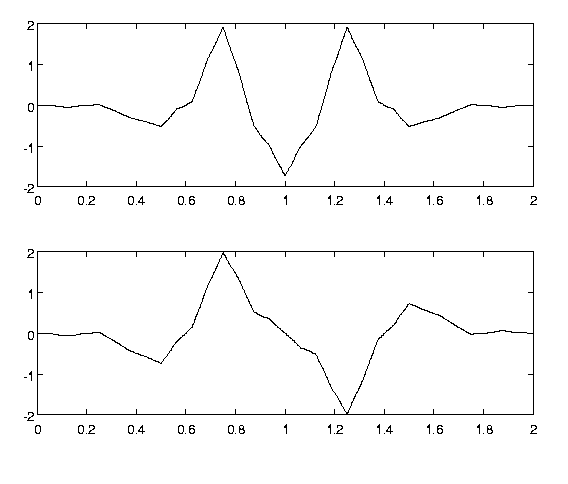
Коэффициенты уравнений рескейлинга таковы:

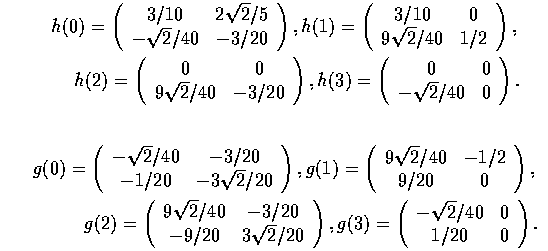
Фильтры, связанные с этими функциями, плохо локализованы по частоте, однако их свойства можно улучшить простой предобработкой сигнала. Совсем недавно Geronimo, Donovan, Hardin получили новое семейство ортогональных мультивйвлетов, которые являются сплайнами с непрерывной производной. Эта конструкция тоже довольно сложна, и использует ортогональные многочлены. Уравнения рескейлинга содержат всего 4 коэффициента, но они являются матрицами (в порядке возрастания гладкости вейвлетов) 4 – 10 порядков. Т.е., в последнем случае есть 10 скейлинг функций и 10 вейвлетов, порождающих соответствующие пространства в МА.