
|
Kantor Ilia
e-mail: algolist@manual.ru
web: http://algolist.manual.ru
Пусть есть последовательность a0, a1... an и функция сравнения, которая на любых двух элементах последовательности принимает одно из трех значений: меньше, больше или равно. Задача сортировки состоит в перестановке членов последовательности таким образом, чтобы выполнялось условие: ai <= ai+1, для всех i от 0 до n.
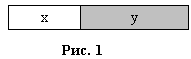
Возможна ситуация, когда элементы состоят из нескольких полей:
 |
struct element {
field x;
field y;
}
|
Если значение функции сравнения зависит только от поля x, то x называют ключом, по которому производится сортировка. На практике, в качестве x часто выступает число, а поле y хранит какие-либо данные, никак не влияющие на работу алгоритма.
Пожалуй, никакая другая проблема не породила такого количества разнообразнейших решений, как задача сортировки. Существует ли некий "универсальный", наилучший алгоритм ? Вообще говоря, нет.
Однако, имея приблизительные характеристики входных данных, можно подобрать метод, работающий оптимальным образом.
Для того, чтобы обоснованно сделать такой выбор, рассмотрим параметры, по которым будет производиться оценка алгоритмов.
- Время сортировки - основной параметр, характеризующий быстродействие алгоритма.
- Память - ряд алгоритмов требует выделения дополнительной памяти под временное хранение данных. При оценке используемой памяти не будет учитываться место, которое занимает исходный массив и независящие от входной последовательности затраты, например, на хранение кода программы.
- Устойчивость - устойчивая сортировка не меняет взаимного расположения равных элементов. Такое свойство может быть очень полезным, если они состоят из нескольких полей, как на рис. 1, а сортировка происходит по одному из них, например, по x.
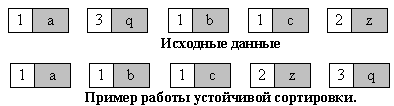 Взаимное расположение равных элементов с ключом 1 и дополнительными полями "a", "b", "c" осталось прежним: элемент с полем "a", затем - с "b", затем - с "c".
Взаимное расположение равных элементов с ключом 1 и дополнительными полями "a", "b", "c" осталось прежним: элемент с полем "a", затем - с "b", затем - с "c".
 Взаимное расположение равных элементов с ключом 1 и дополнительными полями "a", "b", "c" изменилось.
Взаимное расположение равных элементов с ключом 1 и дополнительными полями "a", "b", "c" изменилось.
- Естественность поведения - эффективность метода при обработке уже отсортированных, или частично отсортированных данных. Алгоритм ведет себя естественно, если учитывает эту характеристику входной последовательности и работает лучше.
Еще одним важным свойством алгоритма является его сфера применения. Здесь основных позиций две:
- внутренние сортировки работают с данным в оперативной памяти с произвольным доступом;
- внешние сортировки упорядочивают информацию, расположенную на внешних носителях. Это накладывает некоторые дополнительные ограничения на алгоритм:
- доступ к носителю осуществляется последовательным образом: в каждый момент времени можно считать или записать только элемент, следующий за текущим
- объем данных не позволяет им разместиться в ОЗУ
Кроме того, доступ к данным на носителе производится намного медленнее, чем операции с оперативной памятью.
Данный класс алгоритмов делится на два основных подкласса:
Внутренняя сортировка оперирует с массивами, целиком помещающимися в оперативной памяти с произвольным доступом к любой ячейке. Данные обычно сортируются на том же месте, без дополнительных затрат.
Внешняя сортировка оперирует с запоминающими устройствами большого объема, но с доступом не произвольным, а последовательным (сортировка файлов), т.е в данный момент мы 'видим' только один элемент, а затраты на перемотку по сравнению с памятью неоправданно велики . Это приводит к специальным методам сортировки, обычно использующим дополнительное дисковое пространство.
|

|
Некоторую информацию, которой нет выше, можно найти в FAQ по сортировкам из эхоконференции RU.ALGORITM.
Если же требуется сортировать большие массивы и наложены очень серьезные
требования по быстродейстивю, то весьма хорошее впечатление производит
гибрид быстрой и распределяющей сортировок: "Быстрая сортировка с составными
ключами". В материале сравниваются различные методы сортировки строк и
приводятся исходные тексты на языке C.
Кроме того, существует топологическая сортировка, оперерующая с частично упорядоченными структурами, например, с ориентированными графами без циклов . Она приводит их представление в ЭВМ к виду, при котором все ребра направлены в одну сторону. С циклами такой фокус, естественно, не пройдет.
Информацию о решении родственных сортировке задач можно также найти в разделе: Олимпиадные задачи: сортировки и последовательности.
|